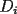1 Scatterplots and Regression
1.1 Scatterplots
1.2 Mean Functions
1.3 Variance Functions
1.4 Summary Graph
1.5 Tools for Looking at Scatterplots
1.5.1 Size
1.5.2 Transformations
1.5.3 Smoothers for the Mean Function
1.6 Scatterplot Matrices
Problems
2 Simple Linear Regression
2.1 Ordinary Least Squares Estimation
2.2 Least Squares Criterion
2.3 Estimating

2.4 Properties of Least Squares Estimates
2.5 Estimated Variances
2.6 Comparing Models: The Analysis of Variance
2.6.1 The F-Test for Regression
2.6.2 Interpreting p-values
2.6.3 Power of Tests
2.7 The Coefficient of Determination,

2.8 Confidence Intervals and Tests
2.8.1 The Intercept
2.8.2 Slope
2.8.3 Prediction
2.8.4 Fitted Values
2.9 The Residuals
Problems
3 Multiple Regression
3.1 Adding a Term to a Simple Linear Regression Model
3.1.1 Explaining Variability
3.1.2 Added-Variable Plots
3.2 The Multiple Linear Regression Model
3.3 Terms and Predictors
3.4 Ordinary Least Squares
3.4.1 Data and Matrix Notation
3.4.2 Variance-Covariance Matrix of e
3.4.3 Ordinary Least Squares Estimators
3.4.4 Properties of the Estimates
3.4.5 Simple Regression in Matrix Terms
3.5 The Analysis of Variance
3.5.1 The Coefficient of Determination
3.5.2 Hypotheses Concerning One of the Terms
3.5.3 Relationship to the t -Statistic
3.5.4 t-Tests and Added-Variable Plots
3.5.5 Other Tests of Hypotheses
3.5.6 Sequential Analysis of Variance Tables
3.6 Predictions and Fitted Values
Problems
4 Drawing Conclusions
4.1 Understanding Parameter Estimates
4.1.1 Rate of Change
4.1.2 Signs of Estimates
4.1.3 Interpretation Depends on Other Terms in the MeanFunction
4.1.4 Rank Deficient and Over-Parameterized Mean Functions
4.1.5 Tests
4.1.6 Dropping Terms
4.1.7 Logarithms
4.2 Experimentation Versus Observation
4.3 Sampling from a Normal Population
4.4 More on
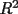
4.4.1 Simple Linear Regression and
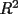
4.4.2 Multiple Linear Regression
4.4.3 Regression through the Origin
4.5 Missing Data
4.5.1 Missing at Random
4.5.2 Alternatives
4.6 Computationally Intensive Methods
4.6.1 Regression Inference without Normality
4.6.2 Nonlinear Functions of Parameters
4.6.3 Predictors Measured with Error
Problems
5 Weights, Lack of Fit, and More
5.1 Weighted Least Squares
5.1.1 Applications of Weighted Least Squares
5.1.2 Additional Comments
5.2 Testing for Lack of Fit, Variance Known
5.3 Testing for Lack of Fit, Variance Unknown
5.4 General F Testing
5.4.1 Non-null Distributions
5.4.2 Additional Comments
5.5 Joint Confidence Regions
Problems
6 Polynomials and Factors
6.1 Polynomial Regression
6.1.1 Polynomials with Several Predictors
6.1.2 Using the Delta Method to Estimate a Minimum or a Maximum
6.1.3 Fractional Polynomials
6.2 Factors
6.2.1 No Other Predictors
6.2.2 Adding a Predictor: Comparing Regression Lines
6.2.3 Additional Comments
6.3 Many Factors
6.4 Partial One-Dimensional Mean Functions
6.5 Random Coefficient Models
Problems
7 Transformations
7.1 Transformations and Scatterplots
7.1.1 Power Transformations
7.1.2 Transforming Only the Predictor Variable
7.1.3 Transforming the Response Only
7.1.4 The Box and Cox Method
7.2 Transformations and Scatterplot Matrices
7.2.1 The 1D Estimation Result and Linearly Related Predictors
7.2.2 Automatic Choice of Transformation of Predictors
7.3 Transforming the Response
7.4 Transformations of Nonpositive Variables
Problems
8 Regression Diagnostics: Residuals
8.1 The Residuals
8.1.1 Difference Between
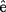
and

8.1.2 The Hat Matrix
8.1.3 Residuals and the Hat Matrix with Weights
8.1.4 The Residuals When the Model Is Correct
8.1.5 The Residuals When the Model Is Not Correct
8.1.6 Fuel Consumption Data
8.2 Testing for Curvature
8.3 Nonconstant Variance
8.3.1 Variance Stabilizing Transformations
8.3.2 A Diagnostic for Nonconstant Variance
8.3.3 Additional Comments
8.4 Graphs for Model Assessment
8.4.1 Checking Mean Functions
8.4.2 Checking Variance Functions
Problems
9 Outliers and Influence
9.1 Outliers
9.1.1 An Outlier Test
9.1.2 Weighted Least Squares
9.1.3 Significance Levels for the Outlier Test
9.1.4 Additional Comments
9.2 Influence of Cases
9.2.1 Cook’s Distance
9.2.2 Magnitude of
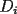
9.2.3 Computing

9.2.4 Other Measures of Influence
9.3 Normality Assumption
Problems
10 Variable Selection
10.1 The Active Terms
10.1.1 Collinearity
10.1.2 Collinearity and Variances
10.2 Variable Selection
10.2.1 Information Criteria
10.2.2 Computationally Intensive Criteria
10.2.3 Using Subject-Matter Knowledge
10.3 Computational Methods
10.3.1 Subset Selection Overstates Significance
10.4 Windmills
10.4.1 Six Mean Functions
10.4.2 A Computationally Intensive Approach
Problems
11 Nonlinear Regression
11.1 Estimation for Nonlinear Mean Functions
11.2 Inference Assuming Large Samples
11.3 Bootstrap Inference
11.4 References
Problems
12 Logistic Regression
12.1 Binomial Regression
12.1.1 Mean Functions for Binomial Regression
12.2 Fitting Logistic Regression
12.2.1 One-Predictor Example
12.2.2 Many Terms
12.2.3 Deviance
12.2.4 Goodness-of-Fit Tests
12.3 Binomial Random Variables
12.3.1 Maximum Likelihood Estimation
12.3.2 The Log-Likelihood for Logistic Regression
Appendix
A.1 Web Site
A.2 Means and Variances of Random Variables
A.2.1 E Notation
A.2.2 Var Notation
A.2.3 Cov Notation
A.2.4 Conditional Moments
A.3 Least Squares for Simple Regression
A.4 Means and Variances of Least Squares Estimates
A.5 Estimating E(Y |X) Using a Smoother,
A.6 A Brief Introduction to Matrices and Vectors
A.6.1 Addition and Subtraction
A.6.2 Multiplication by a Scalar
A.6.3 Matrix Multiplication
A.6.4 Transpose of a Matrix
A.6.5 Inverse of a Matrix
A.6.6 Orthogonality
A.6.7 Linear Dependence and Rank of a Matrix
A.7 Random Vectors
A.8 Least Squares Using Matrices
A.8.1 Properties of Estimates
A.8.2 The Residual Sum of Squares
A.8.3 Estimate of Variance
A.9 The QR Factorization
A.10 Maximum Likelihood Estimates,
A.11 The Box-Cox Method for Transformations
A.11.1 Univariate Case
A.11.2 Multivariate Case
A.12 Case Deletion in Linear Regression


 Jun 12 2007, 09:11 PM
Jun 12 2007, 09:11 PM














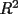
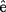 and
and