|
|
|
|
|
|
|
  |
 Nov 21 2020, 03:11 PM Nov 21 2020, 03:11 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.879 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
Sin derivar, encuentre una expansión de Taylor (centrado en 0) hasta el sexto orden de
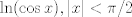 Saludos Claudio. -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 Dec 20 2020, 11:32 PM Dec 20 2020, 11:32 PM
Publicado:
#2
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 82 Registrado: 14-September 19 Desde: Concepción Miembro Nº: 163.344 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Lo había "hecho" hace rato, pero me daba paja resolver el sistema de ecuaciones.
Digamos que 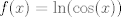 . Enseguida podemos fijarnos que es una función par, por lo tanto la serie de Maclaurin (o Taylor centrada en x=0) solo se compone de términos pares. . Enseguida podemos fijarnos que es una función par, por lo tanto la serie de Maclaurin (o Taylor centrada en x=0) solo se compone de términos pares.Llamamos 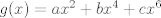 y podemos evaluar la función y podemos evaluar la función 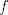 en lugares conocidos (como tiene una función trigonométrica), por ejemplo, en en lugares conocidos (como tiene una función trigonométrica), por ejemplo, en 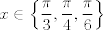 donde la función donde la función 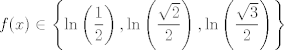 y como queremos una aproximación, podemos igualar y como queremos una aproximación, podemos igualar 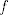 y y 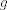 en esos puntos. en esos puntos.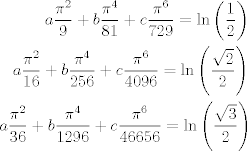 Resolviendo el sistema feo: 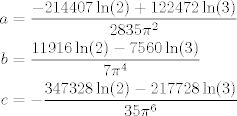  Screenshot_8.png ( 92.02k )
Número de descargas: 2
Screenshot_8.png ( 92.02k )
Número de descargas: 2-------------------- Lo que no te mata, te hace más fuerte.
|
|
|
|
 Dec 21 2020, 09:13 AM Dec 21 2020, 09:13 AM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.879 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
Lo había "hecho" hace rato, pero me daba paja resolver el sistema de ecuaciones. Digamos que 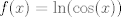 . Enseguida podemos fijarnos que es una función par, por lo tanto la serie de Maclaurin (o Taylor centrada en x=0) solo se compone de términos pares. . Enseguida podemos fijarnos que es una función par, por lo tanto la serie de Maclaurin (o Taylor centrada en x=0) solo se compone de términos pares.Llamamos 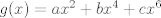 y podemos evaluar la función y podemos evaluar la función 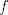 en lugares conocidos (como tiene una función trigonométrica), por ejemplo, en en lugares conocidos (como tiene una función trigonométrica), por ejemplo, en 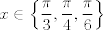 donde la función donde la función 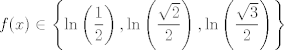 y como queremos una aproximación, podemos igualar y como queremos una aproximación, podemos igualar 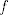 y y 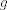 en esos puntos. en esos puntos.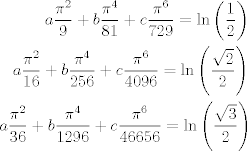 Resolviendo el sistema feo: 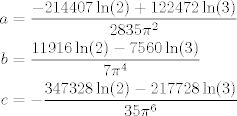  Screenshot_8.png ( 92.02k )
Número de descargas: 2
Screenshot_8.png ( 92.02k )
Número de descargas: 2Uy... que pena. No es lo que se pedía. Lo que hiciste fue encontrar un "polinomio interpolador" (Lagrange), la cual no es la serie de taylor centrada en 0. Sin embargo, no todo es malo. En la primera linea diste información que podría ser relevante para la solución del problema. ¡A seguir intentando! Daré un par de hints: Saludos Claudio. PS: Recomiendo ir al propuesto "Hereda condiciones del limite", podría servir. Mensaje modificado por 2.718281828 el Dec 21 2020, 09:14 AM -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 Dec 21 2020, 01:11 PM Dec 21 2020, 01:11 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 947 Registrado: 28-September 07 Desde: Santiago Miembro Nº: 10.639 Nacionalidad:  Universidad:  Sexo:  |
¿Se espera una solución con usando la O?
Hay una forma super fácil, sale en 1 paso, no se necesita derivar, pero sí integrar Mensaje modificado por Laðeralus el Dec 21 2020, 05:40 PM |
|
|
|
 Dec 22 2020, 01:50 AM Dec 22 2020, 01:50 AM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 524 Registrado: 2-October 13 Miembro Nº: 122.939 Nacionalidad:  Sexo:  |
Sin derivar, encuentre una expansión de Taylor (centrado en 0) hasta el sexto orden de 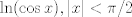 Saludos Claudio. Yo se que tu me vas a matar Claudio por esta pregunta. Pero sabes que me manejo harto menos en calculo que ustedes. Como crestas se encuentra Taylor sin derivar? Formula de la integral de Cauchy quizas? |
|
|
|
 Dec 22 2020, 10:28 AM Dec 22 2020, 10:28 AM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 947 Registrado: 28-September 07 Desde: Santiago Miembro Nº: 10.639 Nacionalidad:  Universidad:  Sexo:  |
Yo se que tu me vas a matar Claudio por esta pregunta. Pero sabes que me manejo harto menos en calculo que ustedes. Como crestas se encuentra Taylor sin derivar? Formula de la integral de Cauchy quizas? Con la O grande se puede, pero pienso que no está a nivel de mechón. Tampoco sé si es la resolución que se espera |
|
|
|
 Dec 22 2020, 10:42 AM Dec 22 2020, 10:42 AM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.879 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
Yo se que tu me vas a matar Claudio por esta pregunta. Pero sabes que me manejo harto menos en calculo que ustedes. Como crestas se encuentra Taylor sin derivar? Formula de la integral de Cauchy quizas? No, como eso... Es cierto que dije "sin derivar", pero me refería a no darse la paja de derivar la función 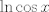 entera. En el fondo igual vamos a usar ciertas series de taylor en las cuales implicitamente hay un previo uso de las derivadas, tanto del coseno como del logaritmo (aunque de esto ultimo es mas integración que derivación), pero son series relativamente conocidas, de ahi viene el asunto de "no derivar". Pero con "no derivar" también implica, como aparece en el hint, usar algún tipo de expansiones u aproximaciones cuando entera. En el fondo igual vamos a usar ciertas series de taylor en las cuales implicitamente hay un previo uso de las derivadas, tanto del coseno como del logaritmo (aunque de esto ultimo es mas integración que derivación), pero son series relativamente conocidas, de ahi viene el asunto de "no derivar". Pero con "no derivar" también implica, como aparece en el hint, usar algún tipo de expansiones u aproximaciones cuando  es chico. es chico.¿Se espera una solución con usando la O? Hay una forma super fácil, sale en 1 paso, no se necesita derivar, pero sí integrar voh dale no mah... con O, integrando, como gustes. -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 Dec 22 2020, 04:13 PM Dec 22 2020, 04:13 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 947 Registrado: 28-September 07 Desde: Santiago Miembro Nº: 10.639 Nacionalidad:  Universidad:  Sexo:  |
voh dale no mah... con O, integrando, como gustes. Me saqué los pillos partiendo con la serie de la tangente. No es muy conocida porque tiene coeficientes feos que son números de Bernoulli, algo así, no me acuerdo bien: ![TEX: \[ \tan(x) = x+\frac{1}{3}x^3 + \frac{2}{15}x^5 + \ldots = x+\frac{1}{3}x^3 + O(x^5) \]](/tex-image/d9b4655b695e75393263eda40145a85d.png) con ![TEX: \[ |x|<\frac{\pi}{2} \]](/tex-image/7301519f4a846358364fc98c2b279f77.png) Integramos, considerando 0 a la constante de integración por ser Taylor centrado en el origen, ![TEX: \[ -\ln(\cos(x)) = \frac{1}{2} x^2+\frac{1}{12}x^4 + O(x^6) \]](/tex-image/b3c8419b50e8fb071e4ff9e9bda35482.png) ![TEX: \[ \ln(\cos(x)) = -\frac{1}{2} x^2 - \frac{1}{12}x^4 - O(x^6) \]](/tex-image/c949eabed61922ff7c96b884c1df322e.png) Esta serie hereda las condiciones de la serie de la tangente y no es w_eveo xd ¿así es? Mensaje modificado por Laðeralus el Dec 23 2020, 12:38 AM |
|
|
|
 Dec 22 2020, 04:18 PM Dec 22 2020, 04:18 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 947 Registrado: 28-September 07 Desde: Santiago Miembro Nº: 10.639 Nacionalidad:  Universidad:  Sexo:  |
Otra forma sería tomar
![TEX: \[ \ln(1+x) = \sum_{n=1}^{\infty} \frac{(-1)^{n+1} x^n}{n} \]](/tex-image/c3d4059ea983dc856d7cea6357bc8a69.png) , cambiar , cambiar  por por 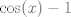 y aplicar el hint de Claudio (creo) y aplicar el hint de Claudio (creo)
Mensaje modificado por Laðeralus el Dec 22 2020, 05:06 PM |
|
|
|
 Dec 23 2020, 04:59 AM Dec 23 2020, 04:59 AM
Publicado:
#10
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 524 Registrado: 2-October 13 Miembro Nº: 122.939 Nacionalidad:  Sexo:  |
Con la O grande se puede, pero pienso que no está a nivel de mechón. Tampoco sé si es la resolución que se espera cuando estuve en primer semestre en fisica, my profe se sacaba aproximaciones de raiz(1+x) por ejemplo con la O, sin derivar (no podia derivar porque no sabiamos) pero alguien me puede confirmar si eso esta bien? Ya ni me acuerdo como lo hacia xD, pero creo que podia sacar que raiz(1+x)=1+x/2+O(x^2) y al parecer podia sacar mas terminos si se lo pedian. Es eso matematicamente correcto? Obviamente no me acuerdo los detalles ya que fue hace como 10 anyos. |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 11:49 PM |





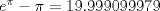
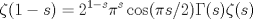







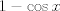 es del orden de
es del orden de 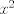 cuando x es pequeño.
cuando x es pequeño.