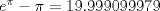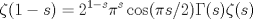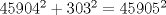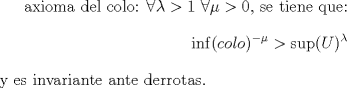Identificarse Registrarse

Psu
Enseñanza Básica
Enseñanza Media
Universidad
Olimpiadas
Comunidad



> sin(1)+sinh(1)
Laðeralus
mensaje Oct 21 2020, 02:44 PM
Publicado: #1


Dios Matemático Supremo
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 947
Registrado: 28-September 07
Desde: Santiago
Miembro Nº: 10.639
Nacionalidad:
Universidad: Universidad Diego Portales
Sexo:



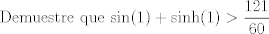
TEX: Demuestre que $\displaystyle \sin(1)+\sinh(1)>\frac{121}{60}$
Go to the top of the page
 
+Quote Post
 
 Start new topic
Respuestas
2.718281828
mensaje Oct 21 2020, 03:11 PM
Publicado: #2


Dios Matemático Supremo
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 1.879
Registrado: 27-December 07
Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR
Miembro Nº: 14.122
Nacionalidad:
Universidad: Universidad Catolica de Chile
Sexo:



¿Es valido usar taylor?. Si es así, de la desigualdad

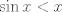TEX: $\sin x<x$ para todo x positivo, integrando 6 veces más, tenemos que:

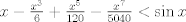TEX: $x-\frac{x^3}{6}+\frac{x^5}{120}-\frac{x^7}{5040}<\sin x$
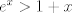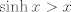Mientras que si x>0, usando el hecho de que TEX: $e^x>1+x$, tenemos que TEX: $\sinh x>x$, como funciones hiperbólicas varían solo entre sinh y cosh sin cambios de signo, es facil ver que integrando 6 veces:

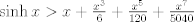TEX: $\sinh x>x+\frac{x^3}{6}+\frac{x^5}{120}+\frac{x^7}{5040}$
De esta manera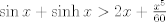
TEX: $\sin x+\sinh x>2x+\frac{x^5}{60}$ donde la desigualdad se obtiene poniendo x=1.
---------------------------------------------------------------
Otra solución bastante parecida, se obtiene notando que 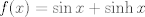TEX: $f(x)=\sin x+\sinh x$ es solucion de la EDO de 4to orden:
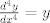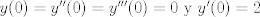TEX: $\frac{d^4 y}{dx^4}=y$ sujeta a TEX: $y(0)=y''(0)=y'''(0)=0$ y $y'(0)=2$. De aqui que su serie de taylor es:
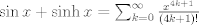TEX: $\sin x+\sinh x=2\sum_{k=0}^{\infty}\frac{x^{4k+1}}{(4k+1)!}$ donde la desigualdad obtenida en la primera parte se obtiene truncando la suma hasta k=1 cuando x>0. (x=1)

Saludos
Claudio.

PD: mas posts así para tapar los post del legi!!!!
PD2: Me pifie en una desigualdad pero ahora sí, esta correcto.

Mensaje modificado por 2.718281828 el Oct 23 2020, 11:35 AM


--------------------
Claudio Henriquez Tapia
Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM
Candidato a Doctor en Estadística UC. Campus San Joaquin
Si todo sale bien, estaría defendiendo en Julio 2024.

[indent]
everywhere at the end of FMAT
ｆｍａｔ　ｎｅｅｄｓ　.... To Survive...
3ch03s facts:

Frases para el bronce by 3ch03s:

Fmat dejame subir mas citas!
TB-3030303
que es YTP-Tennis:
Go to the top of the page
 
+Quote Post
Laðeralus
mensaje Oct 22 2020, 12:38 AM
Publicado: #3


Dios Matemático Supremo
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 947
Registrado: 28-September 07
Desde: Santiago
Miembro Nº: 10.639
Nacionalidad:
Universidad: Universidad Diego Portales
Sexo:



CITA(2.718281828 @ Oct 21 2020, 03:11 PM) *
¿Es valido usar taylor?. Si es así, de la desigualdad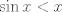

TEX: $\sin x<x$ para todo x positivo, integrando 4 veces más, tenemos que:

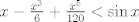TEX: $x-\frac{x^3}{6}+\frac{x^5}{120}<\sin x$
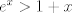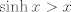Mientras que si x>0, usando el hecho de que TEX: $e^x>1+x$, tenemos que TEX: $\sinh x>x$, como funciones hiperbólicas varían solo entre sinh y cosh sin cambios de signo, es facil ver que integrando 4 veces:

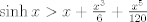TEX: $\sinh x>x+\frac{x^3}{6}+\frac{x^5}{120}$
De esta manera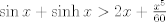
TEX: $\sin x+\sinh x>2x+\frac{x^5}{60}$ donde la desigualdad se obtiene poniendo x=1.
---------------------------------------------------------------
Otra solución bastante parecida, se obtiene notando que 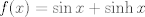TEX: $f(x)=\sin x+\sinh x$ es solucion de la EDO de 4to orden:
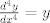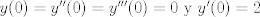TEX: $\frac{d^4 y}{dx^4}=y$ sujeta a TEX: $y(0)=y''(0)=y'''(0)=0$ y $y'(0)=2$. De aqui que su serie de taylor es:
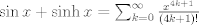TEX: $\sin x+\sinh x=\sum_{k=0}^{\infty}\frac{x^{4k+1}}{(4k+1)!}$ donde la desigualdad obtenida en la primera parte se obtiene truncando la suma hasta k=1 cuando x>0. (x=1)

Saludos
Claudio.

PD: mas posts así para tapar los post del legi!!!!


Sii, yo igual lo hice con series (básicamente es la última parte de la solución con edo)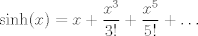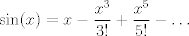
TEX: $\displaystyle \sinh(x)=x+\frac{x^3}{3!}+\frac{x^5}{5!}+\ldots$
TEX: $\displaystyle \sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\ldots$
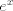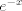La serie de Taylor del seno hiperbólico es fácil sacarla. Tomar la serie de TEX: $e^x$, de TEX: $e^{-x}$, las restas, lo divides por 2 y paff

Para x positivo, las sumamos y tenemos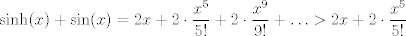
TEX: $\displaystyle \sinh(x) + \sin(x) = 2x + 2\cdot \frac{x^5}{5!}+2\cdot\frac{x^9}{9!}+\ldots > 2x + 2\cdot \frac{x^5}{5!}$
Se pone x=1 y sale

CITA(2.718281828 @ Oct 21 2020, 03:11 PM) *
PD: mas posts así para tapar los post del legi!!!!


looooool

Mensaje modificado por Laðeralus el Oct 22 2020, 12:43 AM
Go to the top of the page
 
+Quote Post
2.718281828
mensaje Oct 23 2020, 11:41 AM
Publicado: #4


Dios Matemático Supremo
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 1.879
Registrado: 27-December 07
Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR
Miembro Nº: 14.122
Nacionalidad:
Universidad: Universidad Catolica de Chile
Sexo:



CITA(Laðeralus @ Oct 22 2020, 12:38 AM) *
Sii, yo igual lo hice con series (básicamente es la última parte de la solución con edo)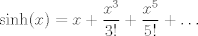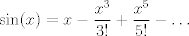
TEX: $\displaystyle \sinh(x)=x+\frac{x^3}{3!}+\frac{x^5}{5!}+\ldots$
TEX: $\displaystyle \sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\ldots$
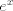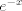La serie de Taylor del seno hiperbólico es fácil sacarla. Tomar la serie de TEX: $e^x$, de TEX: $e^{-x}$, las restas, lo divides por 2 y paff

Para x positivo, las sumamos y tenemos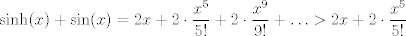
TEX: $\displaystyle \sinh(x) + \sin(x) = 2x + 2\cdot \frac{x^5}{5!}+2\cdot\frac{x^9}{9!}+\ldots > 2x + 2\cdot \frac{x^5}{5!}$
Se pone x=1 y sale
looooool


Acabo de darme cuenta que en la primera solución me pifie en la desigualdad. En efecto, al integrar 2,4 y 6 veces más entre 0 y x ($x \in [0,\pi/2]$) respectivamente: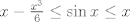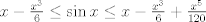

TEX: $x-\frac{x^3}{6} \leq \sin x \leq x$
TEX: $x-\frac{x^3}{6} \leq \sin x \leq x-\frac{x^3}{6} +\frac{x^5}{120}$ (aquí me pifie)
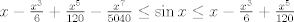TEX: $x-\frac{x^3}{6} +\frac{x^5}{120}-\frac{x^7}{5040} \leq \sin x \leq x-\frac{x^3}{6} +\frac{x^5}{120}$ (desigualdad correcta)

De todas formas lo arregle (idem para el seno hiperbólico) y solo tuve que agregar un término más.

Saludos
Claudio.


--------------------
Claudio Henriquez Tapia
Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM
Candidato a Doctor en Estadística UC. Campus San Joaquin
Si todo sale bien, estaría defendiendo en Julio 2024.

[indent]
everywhere at the end of FMAT
ｆｍａｔ　ｎｅｅｄｓ　.... To Survive...
3ch03s facts:

Frases para el bronce by 3ch03s:

Fmat dejame subir mas citas!
TB-3030303
que es YTP-Tennis:
Go to the top of the page
 
+Quote Post

Mensajes en este tema
Laðeralus   sin(1)+sinh(1)   Oct 21 2020, 02:44 PM
Laðeralus   PD: mas posts así para tapar los post del legi...   Oct 22 2020, 12:19 PM
SuKeVinBellaKo   Legi se va a enojar otra vez conmigo porque puse u...   Oct 23 2020, 11:08 AM

 

Reply to this topicStart new topic
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):

 

Versión Lo-Fi Fecha y Hora actual: 8th April 2025 - 07:24 AM
Powered By IP.Board 2.2.1 © 2007  IPS, Inc.