|
|
|
|
|
|
|
  |
 Nov 16 2005, 09:05 PM Nov 16 2005, 09:05 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Esta olimpiada también estuvo difícil, y a pesar de todo el puntaje más alto fue de 34 puntos. Se entregaron 8 medallas de oro (24 puntos o más), 14 de plata (18 a 23 puntos) y 19 de bronce (10 a 17 puntos), además de 3 menciones de honor (los que resuelven completamente un problema, pero no acumulan puntaje para obtener medalla)
16ª OLIMPIADA IBEROAMERICANA DE MATEMÁTICAS Minas, Uruguay, 2001 Primera Prueba: Martes 25 de Septiembre 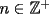 es charrúa si cumple las siguientes condiciones: es charrúa si cumple las siguientes condiciones:
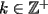 , existe un número charrúa con más de , existe un número charrúa con más de 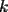 dígitos dígitosProblema 2: El incírculo del 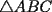 tiene centro tiene centro 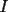 y es tangente a y es tangente a 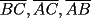 en en 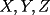 , respectivamente. , respectivamente. 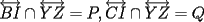 . Pruebe que, si . Pruebe que, si 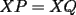 , entonces el , entonces el 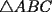 es isósceles. es isósceles.Problema 3: Sean 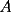 un conjunto con un conjunto con  elementos, y elementos, y 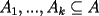 ( (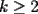 ), cada uno con cardinal mayor o igual que ), cada uno con cardinal mayor o igual que  . Pruebe que . Pruebe que 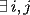 , con , con 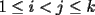 , tales que: , tales que: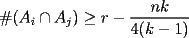 Segunda Prueba: Miércoles 26 de Septiembre 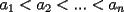 de de 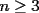 números reales. números reales.Problema 5: En un tablero cuadriculado de 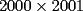 , las casillas tienen coordenadas , las casillas tienen coordenadas 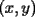 , donde , donde 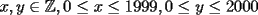 . Una nave en el tablero se mueve de la siguiente manera: antes de cada movimiento, la nave está en una posición . Una nave en el tablero se mueve de la siguiente manera: antes de cada movimiento, la nave está en una posición 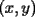 con una velocidad con una velocidad 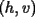 , donde , donde 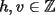 . La nave escoge una nueva velocidad . La nave escoge una nueva velocidad 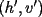 de forma que de forma que 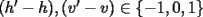 . La nueva posición de la nave será . La nueva posición de la nave será 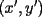 , donde , donde 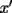 es el resto de dividir es el resto de dividir 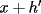 entre 2000 e entre 2000 e 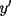 es el resto de dividir es el resto de dividir 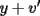 entre 2001. entre 2001.Hay dos naves en el tablero: la marciana y la terrestre, que quiere atrapar a la marciana. Inicialmente, cada nave está en una casilla del tablero, y tiene velocidad 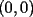 . Primero se mueve la nave terrestre, y continúan moviéndose alternadamente. ¿Existe una estrategia que siempre permita a la nave terrestre atrapar a la nave marciana, cualesquiera que sean las posiciones iniciales? (La nave terrestre, que siempre ve a la marciana, la atrapa si después de un movimiento suyo cae en la misma posición de la marciana. Si la nave marciana, en un movimiento suyo, cae en la misma posición que la nave terrestre, no se produce captura) . Primero se mueve la nave terrestre, y continúan moviéndose alternadamente. ¿Existe una estrategia que siempre permita a la nave terrestre atrapar a la nave marciana, cualesquiera que sean las posiciones iniciales? (La nave terrestre, que siempre ve a la marciana, la atrapa si después de un movimiento suyo cae en la misma posición de la marciana. Si la nave marciana, en un movimiento suyo, cae en la misma posición que la nave terrestre, no se produce captura)Problema 6: Demuestre que es imposible cubrir un cuadrado de lado 1 utilizando cinco cuadrados iguales de lado menor que 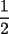 Resumen de soluciones: -------------------- |
|
|
|
 Feb 26 2007, 10:58 AM Feb 26 2007, 10:58 AM
Publicado:
#2
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 374 Registrado: 16-September 06 Desde: New Haven, CT, USA. Miembro Nº: 2.275 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Solución Problema 2:
 screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img338.imageshack.us/img338/5084/figura1kk3.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img338.imageshack.us/img338/5084/figura1kk3.png');}" />![TEX: \[<br />\begin{gathered}<br /> {\text{Notemos que como CI }}{\text{es bisectriz de }}\angle {\text{C y CY = CX}} \Rightarrow {\text{CI es simetral de XY}}{\text{, Luego notamos}} \hfill \\<br /> {\text{que XQ = YQ}}{\text{. Analogamente notamos que BI es simetral de XZ}} \Rightarrow {\text{ZP = XP}} \hfill \\<br /> {\text{Luego como XP = XQ}} \Rightarrow {\text{ZP = XP = XQ = YQ}} \Rightarrow {\text{YQ = ZP}}{\text{, Luego nuestro dibujo esta mal}} \hfill \\<br /> {\text{construido}}{\text{.}} \hfill \\ <br />\end{gathered} <br />\]<br /><br />](./tex/1172505507.gif)  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img153.imageshack.us/img153/3685/figura2zz8.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img153.imageshack.us/img153/3685/figura2zz8.png');}" />![TEX: \[<br />\begin{gathered}<br /> {\text{Con esta figura nueva y el mismo razonamiento llegamos a que YQ = ZP}} \Rightarrow {\text{PY = ZQ}}{\text{.}} \hfill \\<br /> {\text{Trazamos los segmentos IY y IZ}}{\text{, Luego }}\vartriangle IPY \cong \vartriangle IQZ(PY = ZQ;IY = IZ;\angle IYZ = \angle IZY) \hfill \\<br /> \Rightarrow \angle PIY = \angle QIZ,{\text{ Como IY}} \bot {\text{AC y IZ}} \bot {\text{AB}} \Rightarrow \angle IDC{\text{ = }}\angle IEB{\text{ y como }}\angle CID = \angle BIE \hfill \\<br /> \Rightarrow \angle DCI = \angle IBE,{\text{ recordando que CI y BI son bisectrices llegamos a que }}\angle C = \angle B \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/1172505509.gif) Saludos |
|
|
|
 Mar 17 2008, 07:19 PM Mar 17 2008, 07:19 PM
Publicado:
#3
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 2: El incírculo del 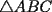 tiene centro tiene centro  y es tangente a y es tangente a 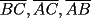 en en 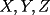 , respectivamente. , respectivamente. 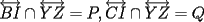 . Pruebe que, si . Pruebe que, si 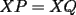 , entonces el , entonces el 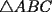 es isósceles. es isósceles.Solución al problema 2 Lema: Considere un triángulo 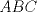 de incentro de incentro 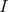 , cuyo incírculo es tangente a , cuyo incírculo es tangente a 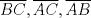 en en 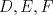 , respectivamente. Sea , respectivamente. Sea 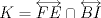 . Entonces . Entonces 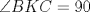 . .Demostración del lema   Comentario: Ojo con el lema, si bien es cierto es simple y de rápida demostración, es bastante útil. Recuerdo que xsebastian me lo dejó de propuesto cuando le pedía hints para un problema de cono sur por ahí Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Apr 1 2008, 08:41 PM Apr 1 2008, 08:41 PM
Publicado:
#4
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 1: Decimos que 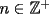 es charrúa si cumple las siguientes condiciones: es charrúa si cumple las siguientes condiciones:
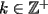 , existe un número charrúa con más de , existe un número charrúa con más de 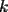 dígitos dígitosSolución al problema 1  Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Apr 2 2008, 02:10 PM Apr 2 2008, 02:10 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Solución al problema 1  Saludos Otra solución correcta -------------------- |
|
|
|
 Feb 11 2009, 10:26 AM Feb 11 2009, 10:26 AM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 1:
Lema: Para cada 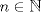 , existe un numero de , existe un numero de  cifras, todas iguales a cifras, todas iguales a 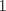 y y 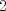 que es multiplo de que es multiplo de 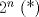 Demostracion:  (*) Este lema se ocupo en la solucion del P6 de la OMCS 2000, y fue el P5 de la final nacional del 2000. Mensaje modificado por ~Fatal_Collapse~ el Aug 16 2010, 09:28 AM -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Feb 11 2009, 05:11 PM Feb 11 2009, 05:11 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Tenemos otra solución correcta para el problema 1, felicitaciones.
-------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 09:04 PM |





 son mayores que 1
son mayores que 1 , se obtiene un divisor de
, se obtiene un divisor de  .
.






