|
|
|
|
|
|
|
  |
 Nov 16 2005, 08:57 PM Nov 16 2005, 08:57 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Un comentario que me hizo un participante (compatriota) de esta olimpiada: con 9 puntos se obtenía la medalla de bronce. Cada problema de olimpiada iberoamericana se califica con puntaje entero, desde 0 hasta 7 (extremos incluidos). A pesar del salto en dificultad, en cualquier caso exisieron varios puntajes buenos.
15ª OLIMPIADA IBEROAMERICANA DE MATEMÁTICAS Caracas, Venezuela, 2000 Primera Prueba: Martes 19 de Septiembre  lados ( lados (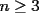 , impar), y se numeran sus vértices, de 1 a , impar), y se numeran sus vértices, de 1 a  . Se trazan todas las diagonales del polígono. Pruebe que es posible asignar a cada lado y a cada diagonal un número en . Se trazan todas las diagonales del polígono. Pruebe que es posible asignar a cada lado y a cada diagonal un número en 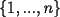 , de modo que: , de modo que:
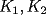 dos circunferencias, de centros dos circunferencias, de centros 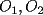 , respectivamente, secantes en , respectivamente, secantes en 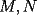 . La recta . La recta 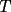 es la tangente común a es la tangente común a 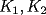 , más cercana a , más cercana a 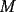 . . 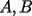 son los respectivos puntos de tangencia de son los respectivos puntos de tangencia de 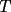 con con 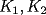 . . 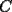 es el punto diametralmente opuesto a es el punto diametralmente opuesto a 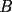 , y , y 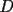 es el punto de intersección de es el punto de intersección de 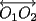 con la recta perpendicular a con la recta perpendicular a 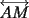 , trazada por , trazada por 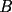 . Pruebe que los puntos . Pruebe que los puntos 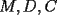 son colineales. son colineales.Problema 3: Encuentre todas las ternas 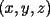 de enteros mayores que 1, tales que: de enteros mayores que 1, tales que: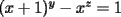 Segunda Prueba: Miércoles 20 de Septiembre 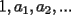 en en 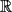 , se eliminan términos, obteniéndose una progresión geométrica infinita de razón , se eliminan términos, obteniéndose una progresión geométrica infinita de razón 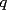 . El 1 no fue eliminado. ¿Qué valores puede tomar . El 1 no fue eliminado. ¿Qué valores puede tomar 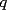 ?. ?.Problema 5: Hay un montón de 2000 piedras. Dos jugadores se turnan para retirar piedras, alternadamente, de acuerdo con las siguientes reglas:
Problema 6: Un hexágono convexo se denomina bonito si tiene cuatro diagonales de longitud 1, cuyos extremos incluyen todos los vértices del hexágono.
-------------------- |
|
|
|
 Apr 5 2007, 03:21 PM Apr 5 2007, 03:21 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Este es uno de los problemas que me mantuvo ocupado por un buen tiempo, pero ahora ya lo he resuelto, hace unos días, estando en Brasil. Digamos que la siguiente demostración es trabajosa, y diría casi con certeza que existe una solución distinta... pueden buscarla
Solución al problema 3 Comenzaremos demostrando algunos resultados interesantes, para usarlos en este problema (oprima el botón "Mostrar") Ahora vamos a resolver nuestro problema. Aplicamos el teorema del Binomio de Newton: 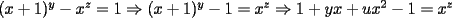 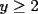 , entonces , entonces 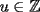 ). Como también ). Como también 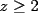 , entonces podemos dividir por , entonces podemos dividir por  : :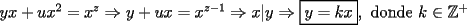 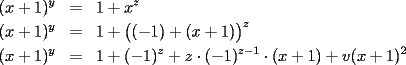 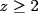 , entonces , entonces 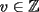 ). Como también ). Como también 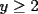 , entonces , entonces 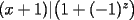 . Pero . Pero 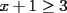 y y 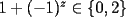 , entonces , entonces 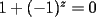 , y así , y así  es impar. Además: es impar. Además: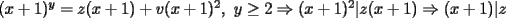  es impar, entonces es impar, entonces 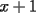 también, y por lo tanto también, y por lo tanto  es par es parAdemás: 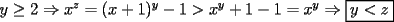 Como 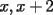 son pares, entonces existen son pares, entonces existen 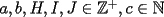 , de modo que , de modo que 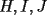 son impares y: son impares y: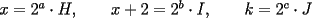 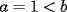 o bien o bien 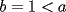 . Ahora, por la proposición 3: como . Ahora, por la proposición 3: como 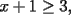 impar, y impar, y 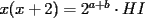 , entonces: , entonces: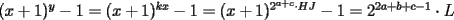 , ,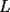 es impar. Esto debe ser igualado con es impar. Esto debe ser igualado con 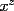 , entonces: , entonces: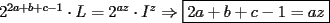 Caso 1: 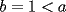 En este caso, 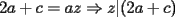 . Aquí usaremos reiteradamente la proposición 1, e indicaremos entre corchetes qué parte estamos usando: . Aquí usaremos reiteradamente la proposición 1, e indicaremos entre corchetes qué parte estamos usando: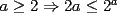 [ a ]. También [ a ]. También 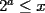 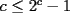 [ c ]. También [ c ]. También 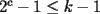 Entonces 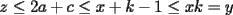 [ d ] (contradicción) [ d ] (contradicción)Caso 2: 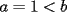 En este caso, 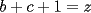 . También usaremos reiteradamente la proposición 1, e indicaremos entre corchetes qué parte estamos usando: . También usaremos reiteradamente la proposición 1, e indicaremos entre corchetes qué parte estamos usando: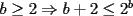 [ b ]. También [ b ]. También 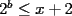 , entonces , entonces 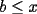 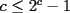 [ c ]. También [ c ]. También 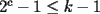 Entonces 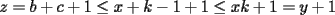 [ d ]. Por lo tanto: [ d ]. Por lo tanto: 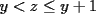 , entonces , entonces 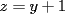 . Como todas las desigualdades se cumplen como igualdades, esto implica algunas cosas: . Como todas las desigualdades se cumplen como igualdades, esto implica algunas cosas: 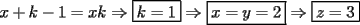 Por lo tanto, la única terna que soluciona nuestro problema, es (2,2,3) PD: No olviden dar una mirada al problema 3', formulado a continuación: Problema 3': Encuentre todas las ternas 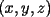 de enteros no negativos, tales que de enteros no negativos, tales que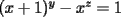 -------------------- |
|
|
|
 Jan 14 2009, 12:39 PM Jan 14 2009, 12:39 PM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Hola. Para el problema 3, creo haber visto alguna vez algo asi como la "conjetura de Catalan". Dice lo siguiente:
La ecuación 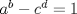 siendo siendo 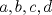 enteros positivos tiene solución unica enteros positivos tiene solución unica 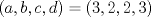 . .Si alguien puede dar más informacíon con respecto a esto estaria agradecido |
|
|
|
 Jan 14 2009, 12:48 PM Jan 14 2009, 12:48 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Si fuese un teorema de Catalán el problema sería trivial, pero si solo es una conjetura, entonces no se ha demostrado su validez o invalidez, por lo tanto el problema tiene sentido de ser propuesto, y se puede utilizar para demostrar la conjetura para el caso especial en que a=c-1.
|
|
|
|
 Jan 14 2009, 12:53 PM Jan 14 2009, 12:53 PM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Si fuese un teorema de Catalán el problema sería trivial, pero si solo es una conjetura, entonces no se ha demostrado su validez o invalidez, por lo tanto el problema tiene sentido de ser propuesto, y se puede utilizar para demostrar la conjetura para el caso especial en que a=c-1. Claro. Ahora que me pongo a buscar (en español), encontre que fue probada el 2002=2000+2 PD: El nombre "oficial" es Teorema de Mihailescu Mensaje modificado por Felipe_ambuli el Jan 14 2009, 01:05 PM |
|
|
|
 Jan 14 2009, 09:15 PM Jan 14 2009, 09:15 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 2:
 Ibero_2000_p2.png ( 139.5k )
Número de descargas: 6
Ibero_2000_p2.png ( 139.5k )
Número de descargas: 6Sean 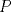 la interseccion de la interseccion de 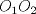 con con 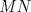 , , 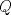 la interseccion de la interseccion de 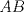 con con 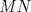 y y 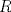 la interseccion de la interseccion de 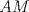 con con 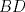 . Primero notemos que . Primero notemos que 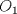 y y 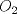 pertenecen a la mediatriz de pertenecen a la mediatriz de 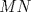 ; es decir, las rectas ; es decir, las rectas 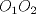 y y 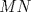 son perpendiculares, luego son perpendiculares, luego 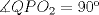 . Por otra parte, como . Por otra parte, como 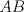 es tangente a es tangente a 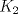 , luego , luego 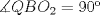 . Se sigue que el . Se sigue que el 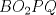 es ciclico, y entonces es ciclico, y entonces 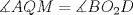 (*). Notemos que (*). Notemos que 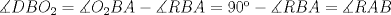 (**). Por (*) y (**), obtenemos que (**). Por (*) y (**), obtenemos que 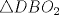 y y 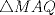 son semejantes. Por otra parte, por potencia de puntos, son semejantes. Por otra parte, por potencia de puntos, 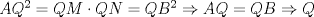 es punto medio de es punto medio de 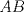 . Ocupando la semejanza de triangulos anteriormente demostrada: . Ocupando la semejanza de triangulos anteriormente demostrada: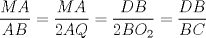 Como 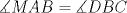 , se sigue que , se sigue que 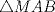 y y 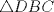 son semejantes. Luego son semejantes. Luego 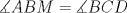 . Por otro lado, notemos que como . Por otro lado, notemos que como 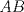 es tangente a es tangente a 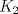 en en 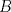 , , 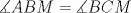 . Por lo tanto . Por lo tanto 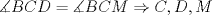 son colineales. son colineales.Espero que este bien. Saludos -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Jan 15 2009, 06:58 PM Jan 15 2009, 06:58 PM
Publicado:
#7
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 2:  Ibero_2000_p2.png ( 139.5k )
Número de descargas: 6
Ibero_2000_p2.png ( 139.5k )
Número de descargas: 6Sean 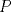 la interseccion de la interseccion de 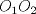 con con 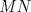 , , 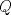 la interseccion de la interseccion de 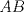 con con 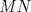 y y 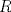 la interseccion de la interseccion de 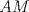 con con 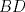 . Primero notemos que . Primero notemos que 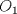 y y 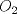 pertenecen a la mediatriz de pertenecen a la mediatriz de 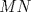 ; es decir, las rectas ; es decir, las rectas 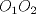 y y 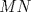 son perpendiculares, luego son perpendiculares, luego 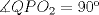 . Por otra parte, como . Por otra parte, como 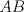 es tangente a es tangente a 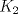 , luego , luego 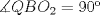 . Se sigue que el . Se sigue que el 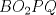 es ciclico, y entonces es ciclico, y entonces 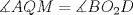 (*). Notemos que (*). Notemos que 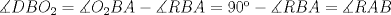 (**). Por (*) y (**), obtenemos que (**). Por (*) y (**), obtenemos que 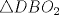 y y 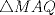 son semejantes. Por otra parte, por potencia de puntos, son semejantes. Por otra parte, por potencia de puntos, 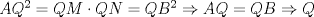 es punto medio de es punto medio de 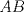 . Ocupando la semejanza de triangulos anteriormente demostrada: . Ocupando la semejanza de triangulos anteriormente demostrada: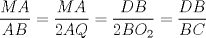 Como 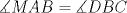 , se sigue que , se sigue que 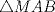 y y 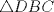 son semejantes. Luego son semejantes. Luego 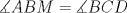 . Por otro lado, notemos que como . Por otro lado, notemos que como 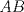 es tangente a es tangente a 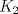 en en 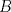 , , 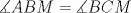 . Por lo tanto . Por lo tanto 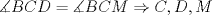 son colineales. son colineales.Espero que este bien. Saludos Solución correctísima, excelente Saludos. -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Jan 16 2009, 06:43 PM Jan 16 2009, 06:43 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.872 Registrado: 9-March 06 Desde: Welcome Miembro Nº: 614 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 5: Hay un montón de 2000 piedras. Dos jugadores se turnan para retirar piedras, alternadamente, de acuerdo con las siguientes reglas:
Un comentario... como yo no le pego mucho a esto, espero que me corrijan con cariño si me equivoqué Llamaremos A al jugador con estrategia ganadora, y B al oponente de A. Además, diremos que N es un numero ganador, si A, dejando N fichas en el tablero, tiene una estrategia para ganar el juego, independiente de la cantidad de piedras que retire B. 0 es, trivialmente, un numero ganador. En segundo lugar, podemos observar que 7 es un numero ganador:  Tercero, observar que 13 es tambien un numero ganador:  De aqui, podemos saltar a la siguiente conjetura: 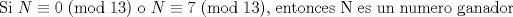 La cual demostraremos por el 2do Principio de Induccion (los casos bases ya fueron presentados). Tratare de ser mas explicativo que formal: H.I: 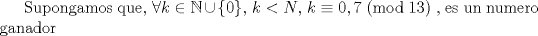 Caso 1. 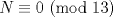 Si B retira p piedras, 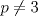 , A puede retirar 6-p piedras respectivamente, llegando a un numero que es congruente a 7 (mod 13). , A puede retirar 6-p piedras respectivamente, llegando a un numero que es congruente a 7 (mod 13).Si B retira 3 piedras, entonces A retira 5 piedras, impidiendo que B pueda retirar la misma cantidad de piedras. Ante lo cual, la jugada de B es retirar q piedras ( 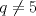 ), y por consiguiente, A, retirando 5-q piedras, cae en un numero congruente a 0 modulo 13. ), y por consiguiente, A, retirando 5-q piedras, cae en un numero congruente a 0 modulo 13.Caso 2. 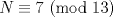 Si B retira $p$ piedras, 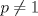 entonces A puede retirar 7-p piedras para caer en el numero congruente a 0 modulo 13. entonces A puede retirar 7-p piedras para caer en el numero congruente a 0 modulo 13.Si B retira 1 piedra, entonces A puede retirar 3 piedras. La siguiente jugada, si B retira 1 o 2 piedras, A puede dejar la mesa con un numero de piedras congruentes a 0 modulo 13, retirando 2 o 1 piedras respectivamente. Si retira 4 o 5, A puede dejar la mesa con un numero de piedras congruentes a 7 modulo 13 (jugando 5 y 4, respectivamente) Por lo tanto, una estrategia ganadora sera mantener el juego dentro de los numeros congruentes a 0 o 7 modulo 13. Así, buscaremos el mayor numero ganador, menor a 2000. 2000: 13 = 153 y resto 11, es decir 1989 es multiplo de 13, y por consiguiente, 1996 es el numero ganador mas cercano a 2000 bajo nuestra estrategia. Tras lo cual, se concluye que el jugador que comienza el juego ganará, retirando 4 piedras en la primera jugada y siguiendo la estrategia descrita anteriormente. Saludos Mensaje modificado por XaPi el Jan 16 2009, 06:47 PM -------------------- USA MAPLE ANTES QUE L'HOPITAL!!!! --- fan
----------------- CURRICULUM VITAE ----------------- 296 pts en la PSU de Matemáticas Admisión 2010. Estudiante de Primer Año de Licenciatura en Historia, Ciencias Sociales y Filosofía Jurídica U. de Talca VII Region Chile |
|
|
|
 Aug 9 2010, 12:10 PM Aug 9 2010, 12:10 PM
Publicado:
#9
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 1 Registrado: 9-August 10 Miembro Nº: 75.204 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Tengo otra solución para el 3.
CASO 1. x es impar. Tal vez no todos usan mi notación, entonces definamos Vp(x) como el exponente con que p aparece en la factorización primo de x. Entonces por lifting the exponent lemma, si p|x, Vp(xz)=Vp((x+1)y-1)=Vp(x)+Vp(y), y Vp(xz)-Vp(x)=Vp(xz-1) Entonces Vp(xz-1)=Vp(y) para todo p|x y si p no divide a x, entonces Vp(xz-1)=0, entonces Vp(xz-1) es menor o igual a Vp(y) para todo p, entonces xz-1|y, entonces xz-1 es menor o igual a y como no logro insertar cógidos Latex correctamente, voy a poner > para mayor o igual y < para menor o igual. Entonces xx(z-1)<(x+1)x(z-1)-1<(x+1)y-1=xz y no puedo poner doble superíndice entonces imaginen que x(z-1) es xz-1, entonces sacando logaritmo en base x tengo xz-1<z y si x es mayor a 1 (como es impar también es mayor a 2) y z es mayor a 1 no hay soluciones, entonces x es par. CASO 2A x es par y V2(x) es mayor a 1. Entonces, por lifting con 2, V2(xz)=V2((x+1)y-1)=V2(x2+2x)+V2(y)-1=V2(x)+V2(x+2)+V2(y)-1=V2(x)+V2(y)... entonces V2(xz-1)=V2(y), entonces otra vez y es múltiplo de xz-1, hacemos la misma desigualdad del caso 1 y llegamos a que si x es mayor a 2 no hay soluciones, y si x es 2 V2(x)=1, entonces en este caso tampoco hay soluciones CASO 2B. x es par y V2(x)=1, entonces x=2k con k impar, y por lifting, para todo p mayor a 2 Vp(xz-1)<Vp(y), entonces y Vp(kz-1)=Vp(xz-1) para todo p mayor a 2 y para 2 V2(kz-1)=0, entonces y es múltiplo de kz-1, entonces xz=(x+1)y-1>(x+1)k(z-1)-1>xk(z-1) Sacamos log en base x y tenemos z>kz-1 y si k es mayor a 2 eso no es cierto. Y k es impar entonces k=1, entonces x=2. Entonces 3y-1=2z y si z es mayor a 1 necesitamos que 3y-1 sea múltiplo de 4, entonces 3 es 1 mod 4, entonces y es par, y=2n, entonces 3y-1=(3n+1)(3n-1) y si n es mayor a 1, necesitamos 3n-1 múltiplo de 4, entonces n par, y 3n+1 también múltiplo de 4, entonces n impar... y como eso no es posible, n=1, entonces y=2 Reemplazando tengo 2z=32-1=8, entonces z=3 |
|
|
|
 Dec 9 2022, 07:15 AM Dec 9 2022, 07:15 AM
Publicado:
#10
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 97 Registrado: 8-July 21 Desde: Chile Miembro Nº: 167.167 |
Problema 1,
Creo que no es tan complicado. La figura abajo explica en figuras un esquema de enumeración que funciona. La fórmula que asigna números a los segmentos i y j es (n+1)/2*(i+j) [mod n], donde [mod n] se asume entre 1 y n. Entonces, por ejemplo, para n=7, la diagonal entre vértices 5 y 2 se le asigna el número (7+1)/2*(5+2)=24≣7 [mod 7], etc. 
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 11:25 AM |





![TEX: $k\in\,]0,1]$](./tex/82501.gif) , encuentre un hexágono bonito de área
, encuentre un hexágono bonito de área 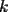
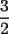



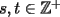 , con
, con 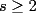 , y sea
, y sea 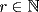 (considere 0 como número natural). Entonces:
(considere 0 como número natural). Entonces: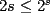 , con igualdad sólo si
, con igualdad sólo si 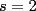
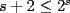 , con igualdad sólo si
, con igualdad sólo si 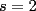
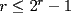 , con igualdad sólo si
, con igualdad sólo si 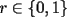
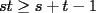 , con igualdad sólo si
, con igualdad sólo si 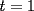
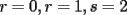 y luego establezca las desigualdades estrictas para
y luego establezca las desigualdades estrictas para 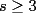 y
y 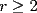 ) (ejercicio al lector). Podemos notar que la parte b es corolario de la parte a. Para la parte d:
) (ejercicio al lector). Podemos notar que la parte b es corolario de la parte a. Para la parte d: 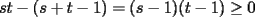 , con igualdad sólo si
, con igualdad sólo si 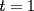 (pues
(pues 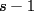 es positivo)
es positivo) 
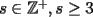 , impar, tal que
, impar, tal que 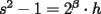 , donde
, donde 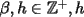 impar. Entonces, para todo
impar. Entonces, para todo 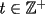 , tenemos que
, tenemos que 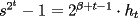 , con
, con 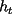 impar
impar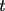 )
)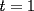 (haga
(haga 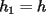 ). Suponga que es verdad para algún
). Suponga que es verdad para algún 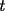 . Entonces:
. Entonces: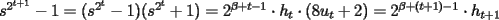 ,
,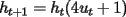 es impar.
es impar. 
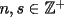 tales que
tales que 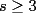 , impar,
, impar, 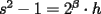 (
(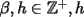 impar) y
impar) y 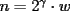 (
(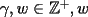 impar).(obvio que
impar).(obvio que  es par). Entonces
es par). Entonces 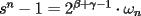 , con
, con 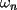 impar.
impar.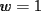 , esto se reduce a la proposición 2. Supongamos
, esto se reduce a la proposición 2. Supongamos 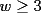 . Entonces:
. Entonces: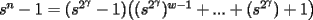
 sumandos, todos impares. Entonces:
sumandos, todos impares. Entonces: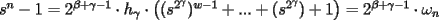 ,
,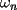 es impar.
es impar. 



