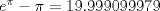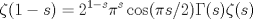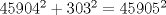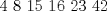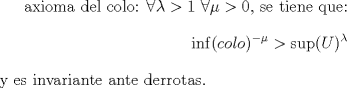|
|
|
|
|
|
|
  |
 May 16 2020, 07:04 PM May 16 2020, 07:04 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.879 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
Calcule:
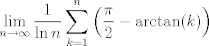 Saludos Claudio. Mensaje modificado por 2.718281828 el May 16 2020, 07:05 PM -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 Nov 15 2020, 02:02 PM Nov 15 2020, 02:02 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.566 Registrado: 20-June 11 Desde: Region del Maule Miembro Nº: 90.738 Sexo:  |
-------------------- Actualmente en Ingenieria Industrial y en 3er año Ingeniería Civil Mecánica.
From my personal life: I highly recommend this video Click Here! Es altamente deseable tener aptitud para la quimica(termodinámica), la programación, alta comprensión de un problema y planteamiento del mismo, y tener resiliencia al estudiar Ingenieria Civil Industrial. Civil Industrial es en gran parte saber levantar(modelar problemas) procesos logísticos. Puedo dar fe que la Universidad Nacional Andres Bello está adelante de varias U'es Regionales(Calidad similar a la UTAL). Realidad universidades del mundo (18:30): Youtube Quiten Filosofia, Musica y Religión del Curriculum de la Media!! No es recomendado trabajar/colaborar entre matemáticos en general. En general, y a menos que Chile gaste mínimo 2% PIB en I+D, quedarse a investigar en el país, es matarse académicamente. Como recomendación Brasil es un pais muy adelantado en investigación versus AL. Gasto 2023: 0,34%.  |
|
|
|
 Nov 15 2020, 02:06 PM Nov 15 2020, 02:06 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.566 Registrado: 20-June 11 Desde: Region del Maule Miembro Nº: 90.738 Sexo:  |
![TEX: \[\begin{array}{l}<br />0 \le \sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le n\pi {\rm{ /Paso trucho *}}\frac{1}{{\ln n}}\\<br />0 \le \sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le \frac{{n\pi }}{{\ln n}}{\rm{ /}}\lim \\<br />0 \le \mathop {\lim \frac{1}{{\ln n}}}\limits_{n \to \infty } \sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le \mathop {\lim }\limits_{n \to \infty } \frac{{n\pi }}{{\ln n}}{\rm{ }}\\<br />0 \le \mathop {\lim }\limits_{n \to \infty } \frac{1}{{\ln n}}\sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le \mathop {\lim }\limits_{n \to \infty } {\rm{ }}n\pi \\<br />0 \le \mathop {\lim }\limits_{n \to \infty } \frac{1}{{\ln n}}\sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le \infty <br />\end{array}\]](/tex-image/bcff99f73eafc640f5e7e0dfa9c45e95.png)
-------------------- Actualmente en Ingenieria Industrial y en 3er año Ingeniería Civil Mecánica.
From my personal life: I highly recommend this video Click Here! Es altamente deseable tener aptitud para la quimica(termodinámica), la programación, alta comprensión de un problema y planteamiento del mismo, y tener resiliencia al estudiar Ingenieria Civil Industrial. Civil Industrial es en gran parte saber levantar(modelar problemas) procesos logísticos. Puedo dar fe que la Universidad Nacional Andres Bello está adelante de varias U'es Regionales(Calidad similar a la UTAL). Realidad universidades del mundo (18:30): Youtube Quiten Filosofia, Musica y Religión del Curriculum de la Media!! No es recomendado trabajar/colaborar entre matemáticos en general. En general, y a menos que Chile gaste mínimo 2% PIB en I+D, quedarse a investigar en el país, es matarse académicamente. Como recomendación Brasil es un pais muy adelantado en investigación versus AL. Gasto 2023: 0,34%.  |
|
|
|
 Nov 15 2020, 02:06 PM Nov 15 2020, 02:06 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.566 Registrado: 20-June 11 Desde: Region del Maule Miembro Nº: 90.738 Sexo:  |
![TEX: \[\begin{array}{l}<br />0 \le \sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le n\pi {\rm{ /Paso trucho *}}\frac{1}{{\ln n}}\\<br />0 \le \sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le \frac{{n\pi }}{{\ln n}}{\rm{ /}}\lim \\<br />0 \le \mathop {\lim \frac{1}{{\ln n}}}\limits_{n \to \infty } \sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le \mathop {\lim }\limits_{n \to \infty } \frac{{n\pi }}{{\ln n}}{\rm{ }}\\<br />0 \le \mathop {\lim }\limits_{n \to \infty } \frac{1}{{\ln n}}\sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le \mathop {\lim }\limits_{n \to \infty } {\rm{ }}n\pi \\<br />0 \le \mathop {\lim }\limits_{n \to \infty } \frac{1}{{\ln n}}\sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le \infty <br />\end{array}\]](/tex-image/ef07784012a2f23374bc230ac61f0648.png)
-------------------- Actualmente en Ingenieria Industrial y en 3er año Ingeniería Civil Mecánica.
From my personal life: I highly recommend this video Click Here! Es altamente deseable tener aptitud para la quimica(termodinámica), la programación, alta comprensión de un problema y planteamiento del mismo, y tener resiliencia al estudiar Ingenieria Civil Industrial. Civil Industrial es en gran parte saber levantar(modelar problemas) procesos logísticos. Puedo dar fe que la Universidad Nacional Andres Bello está adelante de varias U'es Regionales(Calidad similar a la UTAL). Realidad universidades del mundo (18:30): Youtube Quiten Filosofia, Musica y Religión del Curriculum de la Media!! No es recomendado trabajar/colaborar entre matemáticos en general. En general, y a menos que Chile gaste mínimo 2% PIB en I+D, quedarse a investigar en el país, es matarse académicamente. Como recomendación Brasil es un pais muy adelantado en investigación versus AL. Gasto 2023: 0,34%.  |
|
|
|
 Nov 15 2020, 02:13 PM Nov 15 2020, 02:13 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.566 Registrado: 20-June 11 Desde: Region del Maule Miembro Nº: 90.738 Sexo:  |
![TEX: \[\begin{array}{l}<br />\mathop {\lim }\limits_{n \to \infty } (\frac{{{\mathop{\rm arccot}\nolimits} 1}}{{\ln n}} + \frac{{{\mathop{\rm arccot}\nolimits} 2}}{{\ln n}} + \frac{{{\mathop{\rm arccot}\nolimits} 3}}{{\ln n}}... + \frac{{{\mathop{\rm arccot}\nolimits} n}}{{\ln n}})\\<br />(\frac{{{\mathop{\rm arccot}\nolimits} n}}{{\ln n}})' = \frac{{ - \frac{1}{{1 + {n^2}}}}}{{\frac{1}{n}}} = - \frac{n}{{1 + {n^2}}} = \frac{{ - \frac{n}{{{n^2}}}}}{{\frac{{1 + {n^2}}}{{{n^2}}}}} = \frac{0}{1}<br />\end{array}\]](/tex-image/f8d7e11d9515c0cb676cc36efdd58dae.png) Esta medio trucho pero creo que esta bien Mensaje modificado por Legition Rompediskoteqa el Nov 15 2020, 02:14 PM -------------------- Actualmente en Ingenieria Industrial y en 3er año Ingeniería Civil Mecánica.
From my personal life: I highly recommend this video Click Here! Es altamente deseable tener aptitud para la quimica(termodinámica), la programación, alta comprensión de un problema y planteamiento del mismo, y tener resiliencia al estudiar Ingenieria Civil Industrial. Civil Industrial es en gran parte saber levantar(modelar problemas) procesos logísticos. Puedo dar fe que la Universidad Nacional Andres Bello está adelante de varias U'es Regionales(Calidad similar a la UTAL). Realidad universidades del mundo (18:30): Youtube Quiten Filosofia, Musica y Religión del Curriculum de la Media!! No es recomendado trabajar/colaborar entre matemáticos en general. En general, y a menos que Chile gaste mínimo 2% PIB en I+D, quedarse a investigar en el país, es matarse académicamente. Como recomendación Brasil es un pais muy adelantado en investigación versus AL. Gasto 2023: 0,34%.  |
|
|
|
 Nov 15 2020, 02:41 PM Nov 15 2020, 02:41 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.566 Registrado: 20-June 11 Desde: Region del Maule Miembro Nº: 90.738 Sexo:  |
Para despejar el paso trucho
![TEX: \[\begin{array}{l}<br />\mathop {\lim }\limits_{n \to \infty } (\frac{{{\mathop{\rm arccot}\nolimits} 1}}{{\ln n}} + \frac{{{\mathop{\rm arccot}\nolimits} 2}}{{\ln n}} + \frac{{{\mathop{\rm arccot}\nolimits} 3}}{{\ln n}}... + \frac{{{\mathop{\rm arccot}\nolimits} n}}{{\ln n}} + \sum\limits_{k = 1}^n {(\frac{{{\mathop{\rm arccot}\nolimits} n + k}}{{\ln n}}} )\\<br />(\frac{{{\mathop{\rm arccot}\nolimits} n}}{{\ln n}})' + \sum\limits_{k = 1}^n {(\frac{{{\mathop{\rm arccot}\nolimits} n + k}}{{\ln n}}} ) = \frac{{ - \frac{1}{{1 + {n^2}}}}}{{\frac{1}{n}}} + \frac{{ - \frac{1}{{1 + {{(n + k)}^2}}}}}{{\frac{1}{n}}} = - \frac{n}{{1 + {n^2}}} - \sum\limits_{k = 1}^n {\frac{{\frac{1}{{1 + {{(n + k)}^2}}}}}{{\frac{1}{n}}}} = \frac{{ - \frac{n}{{{n^2}}}}}{{\frac{{1 + {n^2}}}{{{n^2}}}}} + \sum\limits_{k = 1}^n {\frac{n}{{1 + {{(n + k)}^2}}}} \\<br /> = \frac{0}{1} + \sum\limits_{k = 1}^n {\frac{n}{{1 + {n^2} + 2nk + {k^2}}}} \\<br /> = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{k = 1}^n {\frac{n}{{\frac{1}{k} + \frac{{{n^2}}}{k} + 2n + k}}} \frac{1}{k}<br />\end{array}\]](/tex-image/e9c7ee4c5422759069be0016c68e901f.png) Algun tip de como pasarla a integral?. -------------------- Actualmente en Ingenieria Industrial y en 3er año Ingeniería Civil Mecánica.
From my personal life: I highly recommend this video Click Here! Es altamente deseable tener aptitud para la quimica(termodinámica), la programación, alta comprensión de un problema y planteamiento del mismo, y tener resiliencia al estudiar Ingenieria Civil Industrial. Civil Industrial es en gran parte saber levantar(modelar problemas) procesos logísticos. Puedo dar fe que la Universidad Nacional Andres Bello está adelante de varias U'es Regionales(Calidad similar a la UTAL). Realidad universidades del mundo (18:30): Youtube Quiten Filosofia, Musica y Religión del Curriculum de la Media!! No es recomendado trabajar/colaborar entre matemáticos en general. En general, y a menos que Chile gaste mínimo 2% PIB en I+D, quedarse a investigar en el país, es matarse académicamente. Como recomendación Brasil es un pais muy adelantado en investigación versus AL. Gasto 2023: 0,34%.  |
|
|
|
 Nov 15 2020, 04:56 PM Nov 15 2020, 04:56 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.879 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
Claramente pasaste de una desigualdad trivial, a otra desigualdad trivial estimado. Tu desarrollo estuvo condenado desde el inicio.
Solo en la primera linea del primer post esta la clave. no basta con desigualdades triviales, hay que escarbar un poco mas. Saludos. -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 Nov 16 2020, 08:07 AM Nov 16 2020, 08:07 AM
Publicado:
#8
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 524 Registrado: 2-October 13 Miembro Nº: 122.939 Nacionalidad:  Sexo:  |
![TEX: \[\begin{array}{l}<br />\frac{\pi }{2} - \arctan (x) = \arctan (\frac{1}{x}) = {\mathop{\rm arccot}\nolimits} (x)\\<br />0 \le {\mathop{\rm arccot}\nolimits} (x) \le \pi {\rm{ }}/\sum {} \\<br />0 \le \sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le \sum\limits_1^n \pi \\<br />0 \le \sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le n\pi <br />\end{array}\]](/tex-image/40455eb8a107ceb68b838352bfa1b7f3.png) y ahi voy ![TEX: \[\begin{array}{l}<br />0 \le \sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le n\pi {\rm{ /Paso trucho *}}\frac{1}{{\ln n}}\\<br />0 \le \sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le \frac{{n\pi }}{{\ln n}}{\rm{ /}}\lim \\<br />0 \le \mathop {\lim \frac{1}{{\ln n}}}\limits_{n \to \infty } \sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le \mathop {\lim }\limits_{n \to \infty } \frac{{n\pi }}{{\ln n}}{\rm{ }}\\<br />0 \le \mathop {\lim }\limits_{n \to \infty } \frac{1}{{\ln n}}\sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le \mathop {\lim }\limits_{n \to \infty } {\rm{ }}n\pi \\<br />0 \le \mathop {\lim }\limits_{n \to \infty } \frac{1}{{\ln n}}\sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le \infty <br />\end{array}\]](/tex-image/bcff99f73eafc640f5e7e0dfa9c45e95.png) ![TEX: \[\begin{array}{l}<br />0 \le \sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le n\pi {\rm{ /Paso trucho *}}\frac{1}{{\ln n}}\\<br />0 \le \sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le \frac{{n\pi }}{{\ln n}}{\rm{ /}}\lim \\<br />0 \le \mathop {\lim \frac{1}{{\ln n}}}\limits_{n \to \infty } \sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le \mathop {\lim }\limits_{n \to \infty } \frac{{n\pi }}{{\ln n}}{\rm{ }}\\<br />0 \le \mathop {\lim }\limits_{n \to \infty } \frac{1}{{\ln n}}\sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le \mathop {\lim }\limits_{n \to \infty } {\rm{ }}n\pi \\<br />0 \le \mathop {\lim }\limits_{n \to \infty } \frac{1}{{\ln n}}\sum\limits_1^n {{\mathop{\rm arccot}\nolimits} (x)} \le \infty <br />\end{array}\]](/tex-image/ef07784012a2f23374bc230ac61f0648.png) ![TEX: \[\begin{array}{l}<br />\mathop {\lim }\limits_{n \to \infty } (\frac{{{\mathop{\rm arccot}\nolimits} 1}}{{\ln n}} + \frac{{{\mathop{\rm arccot}\nolimits} 2}}{{\ln n}} + \frac{{{\mathop{\rm arccot}\nolimits} 3}}{{\ln n}}... + \frac{{{\mathop{\rm arccot}\nolimits} n}}{{\ln n}})\\<br />(\frac{{{\mathop{\rm arccot}\nolimits} n}}{{\ln n}})' = \frac{{ - \frac{1}{{1 + {n^2}}}}}{{\frac{1}{n}}} = - \frac{n}{{1 + {n^2}}} = \frac{{ - \frac{n}{{{n^2}}}}}{{\frac{{1 + {n^2}}}{{{n^2}}}}} = \frac{0}{1}<br />\end{array}\]](/tex-image/f8d7e11d9515c0cb676cc36efdd58dae.png) Esta medio trucho pero creo que esta bien Para despejar el paso trucho ![TEX: \[\begin{array}{l}<br />\mathop {\lim }\limits_{n \to \infty } (\frac{{{\mathop{\rm arccot}\nolimits} 1}}{{\ln n}} + \frac{{{\mathop{\rm arccot}\nolimits} 2}}{{\ln n}} + \frac{{{\mathop{\rm arccot}\nolimits} 3}}{{\ln n}}... + \frac{{{\mathop{\rm arccot}\nolimits} n}}{{\ln n}} + \sum\limits_{k = 1}^n {(\frac{{{\mathop{\rm arccot}\nolimits} n + k}}{{\ln n}}} )\\<br />(\frac{{{\mathop{\rm arccot}\nolimits} n}}{{\ln n}})' + \sum\limits_{k = 1}^n {(\frac{{{\mathop{\rm arccot}\nolimits} n + k}}{{\ln n}}} ) = \frac{{ - \frac{1}{{1 + {n^2}}}}}{{\frac{1}{n}}} + \frac{{ - \frac{1}{{1 + {{(n + k)}^2}}}}}{{\frac{1}{n}}} = - \frac{n}{{1 + {n^2}}} - \sum\limits_{k = 1}^n {\frac{{\frac{1}{{1 + {{(n + k)}^2}}}}}{{\frac{1}{n}}}} = \frac{{ - \frac{n}{{{n^2}}}}}{{\frac{{1 + {n^2}}}{{{n^2}}}}} + \sum\limits_{k = 1}^n {\frac{n}{{1 + {{(n + k)}^2}}}} \\<br /> = \frac{0}{1} + \sum\limits_{k = 1}^n {\frac{n}{{1 + {n^2} + 2nk + {k^2}}}} \\<br /> = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{k = 1}^n {\frac{n}{{\frac{1}{k} + \frac{{{n^2}}}{k} + 2n + k}}} \frac{1}{k}<br />\end{array}\]](/tex-image/e9c7ee4c5422759069be0016c68e901f.png) Algun tip de como pasarla a integral?. siempre se aprende algo nuevo. Lo entendio todo. |
|
|
|
 Nov 16 2020, 08:08 AM Nov 16 2020, 08:08 AM
Publicado:
#9
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 524 Registrado: 2-October 13 Miembro Nº: 122.939 Nacionalidad:  Sexo:  |
Claramente pasaste de una desigualdad trivial, a otra desigualdad trivial estimado. Tu desarrollo estuvo condenado desde el inicio. Solo en la primera linea del primer post esta la clave. no basta con desigualdades triviales, hay que escarbar un poco mas. Saludos. yo creo nuestro intelecto no llega a comprender el hecho de que legi esta haciendo justo lo que hay que hacer |
|
|
|
 Nov 16 2020, 11:08 AM Nov 16 2020, 11:08 AM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
yo creo nuestro intelecto no llega a comprender el hecho de que legi esta haciendo justo lo que hay que hacer legiton=mochizuki? -------------------- blep
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 11:38 PM |