Otra suma de radicales anidados

Otra suma de radicales anidados

Opciones

Laðeralus Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 23 2020, 02:33 AM Publicado: #1
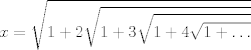
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 947 Registrado: 28-September 07 Desde: Santiago Miembro Nº: 10.639 Nacionalidad: Universidad: Sexo:	Calcule $TEX: $\displaystyle x = \sqrt{1+2\sqrt{1+3\sqrt{1+4\sqrt{1+\ldots}}}}$$

sergio 77 Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 23 2020, 01:01 PM Publicado: #2
Dios Matemático Grupo: Usuario FMAT Mensajes: 408 Registrado: 18-January 11 Desde: soy del colegio san viator de macul no de ovalle. Miembro Nº: 83.168 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: Siguiendo la misma idea que el anterior, consideremos $f\colon {\mathbb{N}} \rightarrow {\mathbb{N}}$ definida por $f(n)=n+1$. Entonces $(\forall n\in {\mathbb{N}})$<br />$f(n)=\sqrt{(n+1)^{2}} = \sqrt{1+n(n+2)}=\sqrt{1+nf(n+1)}$. Luego, $\forall n\in {\mathbb{N}}$,<br />\begin{align}<br />f(n)&=\sqrt{1+n\sqrt{1+(n+1)f(n+2)}}\nonumber\\<br />&=\sqrt{1+n\sqrt{1+(n+1)\sqrt{1+(n+2)f(n+3)}}}\nonumber\\<br />&=\sqrt{1+n\sqrt{1+(n+1)\sqrt{1+(n+2)\sqrt{1+\ldots}}}}<br />\end{align}<br />Por lo que $x=f(2)=3$.<br />$ -------------------- Tercer lugar Olimpiadas del Conocimiento Usach 2011 - Matemáticas

Laðeralus Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 23 2020, 06:18 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 947 Registrado: 28-September 07 Desde: Santiago Miembro Nº: 10.639 Nacionalidad: Universidad: Sexo:	Correcto

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 23rd November 2024 - 04:02 PM