 Evaluar suma rara |
|
|
|
|
|
|
  |
 May 31 2007, 06:35 PM
Publicado:
#1
|
|
 Dios Matemático Supremo  Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:   |
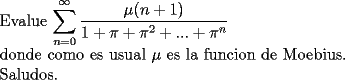
-------------------- Pasten, un buen muchacho en quien confiar.
|
 |
 
|
|
Jun 20 2007, 10:06 PM
Publicado:
#2
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 53 Registrado: 14-May 05 Desde: Santiago de Chile Miembro Nº: 24 Nacionalidad: Colegio/Liceo:  Sexo: |
Notar que:
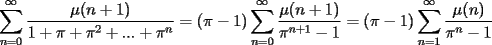 LEMA1: 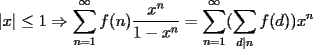 El LEMA1 se probó en la suma satánica, ver aquí. LEMA2: ![TEX: $\displaystyle\sum_{d|n}\mu(d)=\left[\dfrac{1}{n}\right]$](./tex/1182395222.gif) La demostración de este lema se deja como desafio. Ahora se utiliza LEMA1 y LEMA2, así se tiene que: ![TEX: $\displaystyle(\pi-1)\sum_{n=1}^{\infty}\frac{\mu(n)}{\pi^{n}-1}=(\pi-1)\sum_{n=1}^{\infty}\left[\dfrac{1}{n}\right]\dfrac{1}{\pi^{n}}=\dfrac{\pi-1}{\pi}$](./tex/1182395224.gif)
-------------------- Pablo García-|Estudiante de Licenciatura en matemáticas de la Pontificia Universidad Catolica de chile. Ramnujan series: 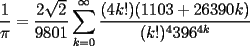 "He looks all over the genius he was."-Hardy |
|
|
|
|
Jun 20 2007, 11:12 PM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad: Sexo: |
Correcto!
Feliz de ver que alguien aprovecha mis propuestos, felicitaciones y a seguir respondiendo. Saludos -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
|
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 09:18 PM |
