duda con EDO Opciones

[diegoh314]

Hola, alguien me podría dar una idea de como resolver este ejercicio
 problem.png ( 48.12k ) Número de descargas:  15

me complica el no saber si tengo que sustituir p(t) por p en u(t) y el u(t) por el u en p(t)
y si u* lo tomo como constante

[Kolmogorov's...]

No es necesario, basta con plantearlo como un sistema de 2x2 y resolverlo con valores propios. El hint huele a algún determinante.

Interesante, es que no es necesario tampoco hacer la parte a) para hacer la b), ya que esta (casi) linealizado el sistema.

[diegoh314]

No es necesario, basta con plantearlo como un sistema de 2x2 y resolverlo con valores propios. El hint huele a algún determinante.

Interesante, es que no es necesario tampoco hacer la parte a) para hacer la b), ya que esta (casi) linealizado el sistema.

y sera posible resolverlo sin un sistema de ecuaciones diferenciales? ya que no vi eso en el curso y se supone que no lo deberían pedir.

[Escalera de penr...]

Es una ecuación acoplada. Deriva una (de preferencia la segunda) y reemplaza en la otra. A las dos condiciones iniciales sumales las ecuaciones originales y con eso obtienes las cuatro constantes de integracion.

[diegoh314]

Es una ecuación acoplada. Deriva una (de preferencia la segunda) y reemplaza en la otra. A las dos condiciones iniciales sumales las ecuaciones originales y con eso obtienes las cuatro constantes de integracion.

tengo dudas de como queda la integral ya que u depende de t y no sé si esta bien  integral.png ( 1.11mb ) Número de descargas:  4

[Escalera de penr...]

tengo dudas de como queda la integral ya que u depende de t y no sé si esta bien  integral.png ( 1.11mb ) Número de descargas:  4

Si u depende de t, entonces t dependerá (para efectos prácticos, implícitamente) de u. Por lo tanto la integración que tienes ahí es en realidad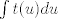



Y si no conoces t{u} no la puedes llevar a a cabo.

A lo que me refería anteriormente es que si derivas la segunda ecuación te queda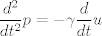



Con puntitos se ve mas claro, pero no se hacerlos en latex. Nota que así obtienes la derivada de u en función de la segunda derivada de p. Y en la segunda ecuación del problena ya tienes u en función de la derivada de p. Por lo tanto reemplazando en la primera ecuación, el u y la derivada de u, obtienes una edo de segundo orden en p.

[Kolmogorov's...]

y sera posible resolverlo sin un sistema de ecuaciones diferenciales? ya que no vi eso en el curso y se supone que no lo deberían pedir.

Como dijo e hizo Escalera, basta reemplazar una ecuación en la otra derivando una y acoplándolas. Te quedará una ecuación de segundo grado, que es equivalente al sistema de 2x2, así que no hay problema, es preguntable.

[diegoh314]

Como dijo e hizo Escalera, basta reemplazar una ecuación en la otra derivando una y acoplándolas. Te quedará una ecuación de segundo grado, que es equivalente al sistema de 2x2, así que no hay problema, es preguntable.

otra cosa que se me olvido decir es que solo nos pasaron ecuaciones diferenciales de primer orden y bernoulli después pasamos a ecuaciones en diferencia así que por eso me extraña que aparezca un ejercicio que se tenga que resolver necesariamente con una EDO de orden superior