Factor Integrante. - Foro fmat.cl

Factor Integrante., Una demostración de factor integrante.

Viper MS Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 21 2018, 11:13 AM Publicado: #1
Principiante Matemático Grupo: Usuario FMAT Mensajes: 2 Registrado: 21-June 18 Miembro Nº: 157.910 Nacionalidad: Sexo:	Alguien podría ayudarme con esta demostración, por favor. Archivo(s) Adjunto(s) IMG_20180621_110926.jpg ( 741.37k ) Número de descargas: 4

Laðeralus Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 21 2018, 01:54 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 947 Registrado: 28-September 07 Desde: Santiago Miembro Nº: 10.639 Nacionalidad: Universidad: Sexo:	Sea 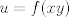$TEX: $u= f(xy)$$ . Entonces $TEX: \[ \frac{\partial \ln(u)}{\partial x} = \frac{f'(xy)}{f(xy)}\cdot y \]$ y $TEX: \[ \frac{\partial \ln(u)}{\partial y} = \frac{f'(xy)}{f(xy)}\cdot x \]$ Por otro lado, recuerda la ecuación del factor integrante: $TEX: \[ \frac{\partial (\ln(u))}{\partial x} N - \frac{\partial (\ln(u))}{\partial y}M = \frac{\partial M}{\partial y} - \frac{\partial N}{\partial x} \]$ Reemplaza los resultados anteriores: $TEX: \[ \frac{f'(xy)}{f(xy)} \left( yN-xM \right) = \frac{\partial M}{\partial y} - \frac{\partial N}{\partial x} \]$ osea $TEX: \[ \frac{\frac{\partial M}{\partial y}-\frac{\partial N}{\partial x}}{yN-xM} = \frac{f'(xy)}{f(xy)} = F(xy) \]$ Asi que en este caso, el factor integrante es 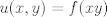$TEX: $u(x,y) = f(xy)$$ donde $TEX: \[ f(z) = e^{\int F(z) dz} \]$ , con z=xy Mensaje modificado por Laðeralus el Jun 21 2018, 01:56 PM

Viper MS Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 22 2018, 08:35 PM Publicado: #3
Principiante Matemático Grupo: Usuario FMAT Mensajes: 2 Registrado: 21-June 18 Miembro Nº: 157.910 Nacionalidad: Sexo:	Ok, creo que sólo hay un pequeño detalle con los signos. Pero muchísimas gracias, yo estaba intentando hacerlo al revés y por supuesto es mucho mejor como tú lo planteas, saludos y agradecimientos.

Laðeralus Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 22 2018, 10:09 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 947 Registrado: 28-September 07 Desde: Santiago Miembro Nº: 10.639 Nacionalidad: Universidad: Sexo:	CITA(Viper MS @ Jun 22 2018, 08:35 PM) Ok, creo que sólo hay un pequeño detalle con los signos. Pero muchísimas gracias, yo estaba intentando hacerlo al revés y por supuesto es mucho mejor como tú lo planteas, saludos y agradecimientos. No encuentro el error de signo. Es exactamente la misma expresión que pusiste en la foto.

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 25th April 2025 - 11:55 PM