 Desigualdad fácil |
|
|
|
|
|
|
Foro fmat.cl > Sector Preparación Olimpiadas > Sector Olímpico > Desigualdades > Problemas Propuestos  |
 May 1 2018, 04:21 PM
Publicado:
#1
|
|
|
Matemático  Grupo: Usuario FMAT Mensajes: 41 Registrado: 10-April 17 Desde: Italia Miembro Nº: 150.783 Sexo:   |
Sean
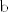 ,  ,  números reales positivos. Probar que![TEX: $ \biggl(1+\frac{a}{b}\biggr) \biggl(1+\frac{b}{c}\biggr) \biggl(1+\frac{c}{a}\biggr) \ge 2 \biggl(1+\frac{a+b+c}{\sqrt[3]{abc}}\biggr). $](/tex-image/9f0a7d08fce97f89b560658ef0338e6f.png)
|
 |
 
|
|
May 4 2018, 08:46 AM
Publicado:
#2
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 52 Registrado: 5-December 12 Miembro Nº: 114.123 Nacionalidad:  Sexo: |
![TEX: Multiplicando el lado izquierdo vemos que la desigualdad es equivalente a<br /><br />$$\frac a b +\frac b c +\frac c a +\frac b a +\frac c b +\frac a c \geq 2\frac{a+b+c}{\sqrt[3]{abc}}$$<br /><br />Ahora considerando $x=\frac{a}{b}, y=\frac{b}{c}$ y $z=\frac{c}{a}$ tenemos $xyz=1$ y como $\frac{a}{\sqrt[3]{abc}}=\sqrt[3]{x^2y}$ la desigualdad original queda <br /><br />$$x+y+z+xy+yz+zx \geq 2(\sqrt[3]{x^2y}+\sqrt[3]{y^2z}+\sqrt[3]{z^2x})$$<br /><br />Finalmente por MA-MG tenemos $$z+x+x \geq 3\sqrt[3]{zx^2} \text{ y } xy+zx+zx\geq 3\sqrt[3]{zx^2}$$ de donde $z+xy+2x+2xz\geq 6\sqrt[3]{zx^2}$. Sumando cíclicamente respecto a $x,y,z$ se obtiene lo pedido.](/tex-image/f309484817406bc843362006e33f19b1.png) No debería estar haciendo esto. |
|
|
|
|
May 4 2018, 01:08 PM
Publicado:
#3
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 41 Registrado: 10-April 17 Desde: Italia Miembro Nº: 150.783 Sexo: |
Muy bién lapantufla. gracias!
|
|
|
|
|
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 12th April 2025 - 09:56 AM |
