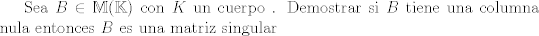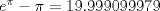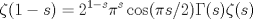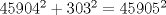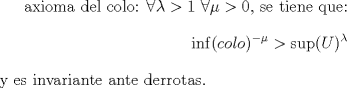|
|
|
|
|
|
|
  |
 Dec 11 2017, 08:14 PM Dec 11 2017, 08:14 PM
Publicado:
#1
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 124 Registrado: 29-September 17 Miembro Nº: 153.951 Nacionalidad:  Sexo:  |
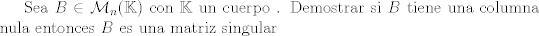
Mensaje modificado por Ignacio.21 el Dec 13 2017, 08:10 PM |
|
|
|
 Dec 12 2017, 10:02 AM Dec 12 2017, 10:02 AM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.566 Registrado: 20-June 11 Desde: Region del Maule Miembro Nº: 90.738 Sexo:  |
disculpa tiene error el tipeo
-------------------- Actualmente en Ingenieria Industrial y en 3er año Ingeniería Civil Mecánica.
From my personal life: I highly recommend this video Click Here! Es altamente deseable tener aptitud para la quimica(termodinámica), la programación, alta comprensión de un problema y planteamiento del mismo, y tener resiliencia al estudiar Ingenieria Civil Industrial. Civil Industrial es en gran parte saber levantar(modelar problemas) procesos logísticos. Puedo dar fe que la Universidad Nacional Andres Bello está adelante de varias U'es Regionales(Calidad similar a la UTAL). Realidad universidades del mundo (18:30): Youtube Quiten Filosofia, Musica y Religión del Curriculum de la Media!! No es recomendado trabajar/colaborar entre matemáticos en general. En general, y a menos que Chile gaste mínimo 2% PIB en I+D, quedarse a investigar en el país, es matarse académicamente. Como recomendación Brasil es un pais muy adelantado en investigación versus AL. Gasto 2023: 0,34%.  |
|
|
|
 Dec 12 2017, 04:35 PM Dec 12 2017, 04:35 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.875 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
-------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 Dec 12 2017, 04:45 PM Dec 12 2017, 04:45 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.875 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
Supongamos que es no singular. si es no singular entonces sus columnas son linealmente independientes, es decir, si
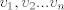 son sus columnas entonces la única combinacion lineal posible que de 0, es la que da ponderaciones 0, es decir: son sus columnas entonces la única combinacion lineal posible que de 0, es la que da ponderaciones 0, es decir: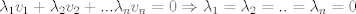 sin perdida de generalidad supongamos que 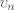 es 0. La contradiccion se da porque hay infinitas combinaciones lineales que den 0, es decir es 0. La contradiccion se da porque hay infinitas combinaciones lineales que den 0, es decir 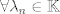 se tiene que se tiene que 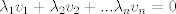 . .Saludos Claudio. Mensaje modificado por 2.718281828 el Dec 12 2017, 04:47 PM -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 Dec 12 2017, 05:02 PM Dec 12 2017, 05:02 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.566 Registrado: 20-June 11 Desde: Region del Maule Miembro Nº: 90.738 Sexo:  |
Otra forma sería tomar el determinante de la columa nula y ver que es 0, por tanto el rango es menor que el mayor orden de la matriz. Por tanto no es invertible, o singular.
-------------------- Actualmente en Ingenieria Industrial y en 3er año Ingeniería Civil Mecánica.
From my personal life: I highly recommend this video Click Here! Es altamente deseable tener aptitud para la quimica(termodinámica), la programación, alta comprensión de un problema y planteamiento del mismo, y tener resiliencia al estudiar Ingenieria Civil Industrial. Civil Industrial es en gran parte saber levantar(modelar problemas) procesos logísticos. Puedo dar fe que la Universidad Nacional Andres Bello está adelante de varias U'es Regionales(Calidad similar a la UTAL). Realidad universidades del mundo (18:30): Youtube Quiten Filosofia, Musica y Religión del Curriculum de la Media!! No es recomendado trabajar/colaborar entre matemáticos en general. En general, y a menos que Chile gaste mínimo 2% PIB en I+D, quedarse a investigar en el país, es matarse académicamente. Como recomendación Brasil es un pais muy adelantado en investigación versus AL. Gasto 2023: 0,34%.  |
|
|
|
 Dec 12 2017, 05:44 PM Dec 12 2017, 05:44 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.875 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
Otra forma sería tomar el determinante de la columa nula y ver que es 0, por tanto el rango es menor que el mayor orden de la matriz. Por tanto no es invertible, o singular. buen intento, Pero ¿cómo definirias el determinante de una matriz que está sobre un cuerpo K?. Saludos Claudio. -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 Dec 12 2017, 09:08 PM Dec 12 2017, 09:08 PM
Publicado:
#7
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 124 Registrado: 29-September 17 Miembro Nº: 153.951 Nacionalidad:  Sexo:  |
|
|
|
|
 Dec 12 2017, 10:23 PM Dec 12 2017, 10:23 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.875 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
Gracias Claudio pero me puedes decir que codigo estaba mal tipeado ? quisiera saber como colocar M_n matrices de orden nxn ? Basicamente te falto colocar los ''$'' en la ecuacion y mathbb es en minuscula. CODE Sea B \in \Mathbb{M} (\mathbb{K}) con K un cuerpo . Demostrar si B tiene una columna nula entonces B es una matriz singular Ahora, usualmente para las matrices uno en vez de utilizar mathbb utiliza por lo general mathcal. El codigo segun lo necesitas dentro del tex sería CODE Sea $B \in \mathcal{M}_n (\mathbb{K})$ con $\mathbb{K}$ un cuerpo . Demostrar si $B$ tiene una columna nula entonces $B$ es una matriz singular Lo cual produce (dentro del Tex) 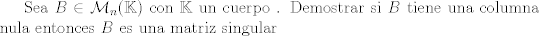 Saludos Claudio. -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 Dec 13 2017, 03:08 PM Dec 13 2017, 03:08 PM
Publicado:
#9
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 394 Registrado: 11-January 12 Miembro Nº: 100.123 Nacionalidad:  Sexo:  |
buen intento, Pero ¿cómo definirias el determinante de una matriz que está sobre un cuerpo K?. Saludos Claudio. Me gustaría saber cómo la defines sobre los reales (o complejos, no sé cuál uses tú) y por qué no funciona eso en un cuerpo arbitrario. Saludos -------------------- |
|
|
|
 Dec 13 2017, 03:13 PM Dec 13 2017, 03:13 PM
Publicado:
#10
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 394 Registrado: 11-January 12 Miembro Nº: 100.123 Nacionalidad:  Sexo:  |
Supongamos que es no singular. si es no singular entonces sus columnas son linealmente independientes, es decir, si 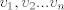 son sus columnas entonces la única combinacion lineal posible que de 0, es la que da ponderaciones 0, es decir: son sus columnas entonces la única combinacion lineal posible que de 0, es la que da ponderaciones 0, es decir: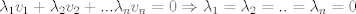 sin perdida de generalidad supongamos que 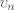 es 0. La contradiccion se da porque hay infinitas combinaciones lineales que den 0, es decir es 0. La contradiccion se da porque hay infinitas combinaciones lineales que den 0, es decir 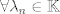 se tiene que se tiene que 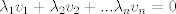 . .Saludos Claudio. No. La contradicción viene de que 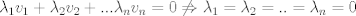 para ver que esta implicancia no se cumple, basta elegir 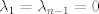 y tomar, por ejemplo, y tomar, por ejemplo, 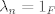 , eso satisface lo de la izquierda pero no lo de la derecha. , eso satisface lo de la izquierda pero no lo de la derecha.Saludos Mensaje modificado por Gastón Burrull el Dec 13 2017, 03:13 PM -------------------- |
|
|
|
  |
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 04:33 PM |