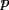|
|
|
|
|
|
|
  |
 Nov 16 2005, 07:56 PM Nov 16 2005, 07:56 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
6ª OLIMPIADA IBEROAMERICANA DE MATEMÁTICAS Problema 1: A cada vértice de un cubo se le asigna un 1 o un -1. Luego, a cada cara se le asigna el producto de los cuatro números asociados a sus vértices. ¿Qué valores puede tomar la suma de los catorce números así obtenidos?Córdoba, Argentina, 1991 Primera Prueba: Septiembre Problema 2: Dos rectas perpendiculares dividen un cuadrado en cuatro partes, tres de las cuales tienen (cada una) área 1. Demuestre que el cuadrado tiene área 4 Problema 3: Sea ![TEX: $f:[0,1]\rightarrow[0,1]$](./tex/79640.gif) una función no decreciente que cumple lo siguiente una función no decreciente que cumple lo siguiente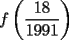 Segunda Prueba: Septiembre  de cinco cifras diferentes y no nulas, que sea igual a la suma de todos los números de tres cifras distintas que se pueden formar con las cinco cifras de de cinco cifras diferentes y no nulas, que sea igual a la suma de todos los números de tres cifras distintas que se pueden formar con las cinco cifras de  Problema 5: Sea 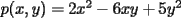 un polinomio en dos variables. Diremos que un polinomio en dos variables. Diremos que 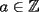 es un <span style='color:red'>valor de</span> es un <span style='color:red'>valor de</span> 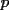 si si 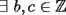 tales que tales que 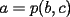
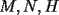 , sabemos que , sabemos que 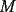 y y 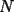 son los puntos medios de dos lados de un triángulo, y que son los puntos medios de dos lados de un triángulo, y que 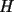 es su ortocentro. Construya el triángulo es su ortocentro. Construya el triánguloResumen de soluciones -------------------- |
|
|
|
 Nov 16 2005, 09:54 PM Nov 16 2005, 09:54 PM
Publicado:
#2
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 293 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 3 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Solucion al problema 5:
notemos ke 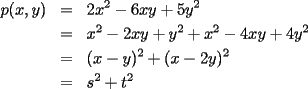 Probaremos la parte de ke el producto de dos valores de 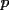 es valor de es valor de 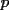 (la parte a es mas facilita (la parte a es mas facilita 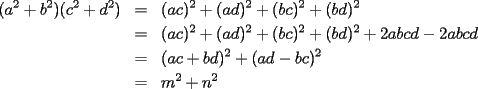 con lo ke keda probado --------------------  |
|
|
|
 Nov 17 2005, 07:22 PM Nov 17 2005, 07:22 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Tú estás afirmando algo con la siguiente igualdad:
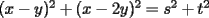 Quieres decir que escribirlo de una forma, es equivalente a escribirlo de la otra. Hay una sutil diferencia entre ambas formas, que debemos evitar de algún modo. Por ejemplo, pudo ser que "por comodidad" escribieras algo del tipo: 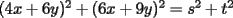 Pero NO es lo mismo que un número tenga la forma del lado izquierdo, a que tenga la forma del lado derecho. Podemos pasar de la izquierda para la derecha, pero no siempre al revés (suponiendo todo entero). Porque el lado izquierdo es: 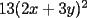 O sea no es equivalente un número de esta forma, con uno que sea suma de dos cuadrados. Otro ejemplo sería si se tuviera: 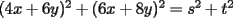 No son dos formas equivalentes, porque el lado izquierdo debe ser par, en cambio el lado derecho admite (en principio) números impares. Aquí hay una pequeña ventaja: 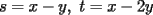 , de donde , de donde 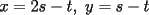 Te faltó una consideración de ese estilo, para entender que los valores de 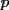 , y las sumas de dos cuadrados perfectos, son precisamente cosas equivalentes. , y las sumas de dos cuadrados perfectos, son precisamente cosas equivalentes.Alguien que intente aclarar este asunto:  es un valor de es un valor de 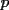 (apegado a la definición) (apegado a la definición) 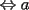 es suma de cuadrados de dos enteros" (observen con cuidado lo que acabo de decir) es suma de cuadrados de dos enteros" (observen con cuidado lo que acabo de decir)Y otro alguien (o el mismo) que HAGA la parte a De lo contrario, no daremos este problema como resuelto -------------------- |
|
|
|
 Nov 28 2005, 03:10 PM Nov 28 2005, 03:10 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
-------------------- |
|
|
|
 Dec 21 2005, 06:16 PM Dec 21 2005, 06:16 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 903 Registrado: 28-May 05 Desde: Santiago, Chile Miembro Nº: 69 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Tengo una gran inquietud en el Problema 3...
Aquí va, quiero que vean si he cometido algún error o qué cosa ocurre: 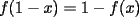 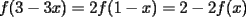 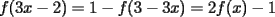 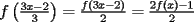 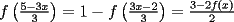 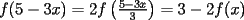 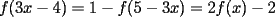 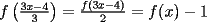 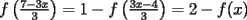 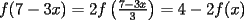 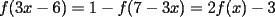 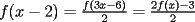 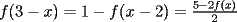 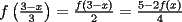 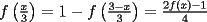 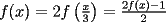 Entonces llegamos a la igualdad 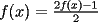 Y desarrollando: 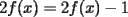 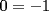 POR QUÉ PASA ESTO??? eso, gracias... -------------------- Bachiller en Ciencias
(ex) Estudiante de Medicina Estudiante de Ingeniería Civil de Industrias, diploma en Ingeniería Matemática Pontificia Universidad Católica de Chile  |
|
|
|
 Dec 21 2005, 08:23 PM Dec 21 2005, 08:23 PM
Publicado:
#6
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
La verdad revisar todo tu desarrollo me dio flojera...jejejeje...pero hay un error claro en tu razonamiento.
La funcion va de ![TEX: $[0,1]$](./tex/4451.gif) en en ![TEX: $[0,1]$](./tex/4452.gif) Si en tu calculo usaste 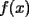 entonces tenemos implicito que entonces tenemos implicito que ![TEX: $x\in[0,1]$](./tex/4449.gif) Ahora si usas  esta implicito que esta implicito que 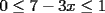 y asi concluyes que y asi concluyes que ![TEX: $x\in[2,\frac{7}{3}]$](./tex/4446.gif) Contradiccion... Quizas hayan mas detalles...ojala alguien quiera revisar mas a fondo Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Dec 21 2005, 09:47 PM Dec 21 2005, 09:47 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 903 Registrado: 28-May 05 Desde: Santiago, Chile Miembro Nº: 69 Nacionalidad:  Colegio/Liceo:  Sexo:  |
aaah ya... igual como q me había dado cuenta...
y algo también... me pueden dar un hint para ese problema? -------------------- Bachiller en Ciencias
(ex) Estudiante de Medicina Estudiante de Ingeniería Civil de Industrias, diploma en Ingeniería Matemática Pontificia Universidad Católica de Chile  |
|
|
|
 Jan 1 2006, 03:37 AM Jan 1 2006, 03:37 AM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Aunque parezca un poco ridículo, el único consejo para el problema 3 es tener harta paciencia. Los argumentos que pusiste antes, como dijo Kenshin, no están muy buenos, según los valores que puede tomar
 Intenta calcular  , para todos los , para todos los  que puedas, a ver si descubres algo interesante que puedas, a ver si descubres algo interesante
-------------------- |
|
|
|
| Corecrasher |
 Feb 28 2006, 07:51 PM Feb 28 2006, 07:51 PM
Publicado:
#9
|
|
Invitado |
 Notemos que cada vez que algun vertice cambia de signo se ven alterados Notemos que cada vez que algun vertice cambia de signo se ven alterados  sumandos de la suma final , el vertice y las sumandos de la suma final , el vertice y las  caras que lo contienen. caras que lo contienen.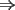 La suma buscada La suma buscada 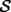 varia de la forma varia de la forma 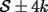 . (*) . (*)Notemos que la maxima suma es 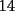 por lo tanto la supuesta minima seria por lo tanto la supuesta minima seria 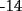 , luego , luego 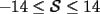 Por (*) los supuestos posibles valores de 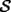 serian: serian: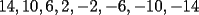 . .Estamos claros que 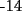 es imposible pues deberian de ser asi todos los vertices negativos y de ser asi las caras positivas. es imposible pues deberian de ser asi todos los vertices negativos y de ser asi las caras positivas.Estamos claros que no se puede obtener 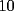 pues si es asi deben haber pues si es asi deben haber 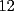 positivos y positivos y  negativos , con un vertice negativo negativos , con un vertice negativo 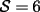 y con dos vertices negativos hay ademas y con dos vertices negativos hay ademas  caras por lo menos negativas , que son las que tienen a uno de los vertices pero no al otro. caras por lo menos negativas , que son las que tienen a uno de los vertices pero no al otro.Luego 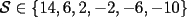 , que seran mostrados acontinuacion para que no pifeen que talvez lo que digo no es verdad , que seran mostrados acontinuacion para que no pifeen que talvez lo que digo no es verdad  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img157.imageshack.us/img157/8086/dibujo8tx.jpg');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img157.imageshack.us/img157/8086/dibujo8tx.jpg');}" />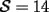 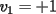 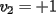 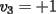 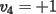 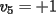 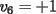 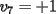 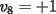 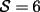 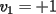 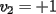 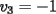 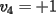 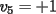 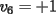 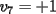 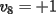 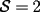 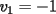 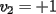 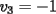 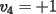 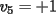 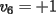 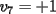 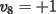 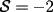 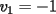 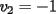 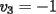 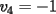 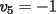 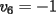 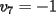 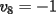 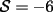 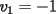 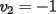 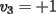 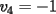 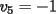 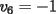 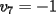 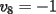 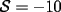 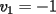 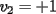 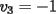 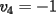 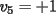 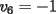 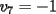 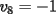 |
|
|
|
| Corecrasher |
 Feb 28 2006, 07:53 PM Feb 28 2006, 07:53 PM
Publicado:
#10
|
|
Invitado |
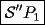 Voy a hacerla cortita en esta segunda solucion , es un poquitin mas intuitiva , solo basta con empezar con un cubo con todos sus vertices del mismo signo e ir cambiando vertice por vertice el signo hasta llegar de tener todos los vertices de un signo hasta el otro signo , asi pasaremos por todos los posibles valores Voy a hacerla cortita en esta segunda solucion , es un poquitin mas intuitiva , solo basta con empezar con un cubo con todos sus vertices del mismo signo e ir cambiando vertice por vertice el signo hasta llegar de tener todos los vertices de un signo hasta el otro signo , asi pasaremos por todos los posibles valores 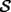 cada vez que cambiemos el signo de un vertice) cada vez que cambiemos el signo de un vertice)
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 08:51 PM |






![TEX: $\forall x\in[0,1]:f\left(\dfrac{x}{3}\right)=\dfrac{f(x)}{2}$](./tex/79642.gif)
![TEX: $\forall x\in[0,1]:f(1-x)=1-f(x)$](./tex/79643.gif)
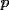
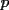 es un valor de
es un valor de