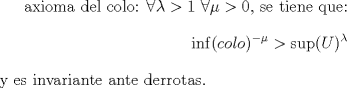|
|
|
|
|
|
|
  |
 Oct 29 2017, 04:00 PM Oct 29 2017, 04:00 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.566 Registrado: 20-June 11 Desde: Region del Maule Miembro Nº: 90.738 Sexo:  |
Hola les traigo este ejercicio, porque no veo una forma de sacar el limite sin l'hopital.
![TEX: \[\mathop {\lim }\limits_{x \to 1} \frac{{x - senx}}{{{x^3}}}\]](/tex-image/39ca6144d83e3f1b273021c35713b0bc.png)
-------------------- Actualmente en Ingenieria Industrial y en 3er año Ingeniería Civil Mecánica.
From my personal life: I highly recommend this video Click Here! Es altamente deseable tener aptitud para la quimica(termodinámica), la programación, alta comprensión de un problema y planteamiento del mismo, y tener resiliencia al estudiar Ingenieria Civil Industrial. Civil Industrial es en gran parte saber levantar(modelar problemas) procesos logísticos. Puedo dar fe que la Universidad Nacional Andres Bello está adelante de varias U'es Regionales(Calidad similar a la UTAL). Realidad universidades del mundo (18:30): Youtube Quiten Filosofia, Musica y Religión del Curriculum de la Media!! No es recomendado trabajar/colaborar entre matemáticos en general. En general, y a menos que Chile gaste mínimo 2% PIB en I+D, quedarse a investigar en el país, es matarse académicamente. Como recomendación Brasil es un pais muy adelantado en investigación versus AL. Gasto 2023: 0,34%.  |
|
|
|
 Oct 29 2017, 04:58 PM Oct 29 2017, 04:58 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.875 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
Hola les traigo este ejercicio, porque no veo una forma de sacar el limite sin l'hopital. ![TEX: \[\mathop {\lim }\limits_{x \to 1} \frac{{x - senx}}{{{x^3}}}\]](/tex-image/39ca6144d83e3f1b273021c35713b0bc.png) vaya vaya... como te animas a ganarte tus porotitos!!! bien, bien! ojala pprimo te viera y cambie esa opinion tan toxica que tiene, asi como tu reputación en el foro. o x tiende a 1 o bien x tiende a 0. si x tiende a 1 es evaluar directo. si x tiende a 0 (que es mas interesante) existe la opcion de expandir el seno por taylor: 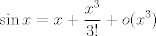 (alguien rectifique si esta bien el orden del o chico.) (alguien rectifique si esta bien el orden del o chico.)de esta forma obtienes 1/6. La otra opcion que se me ocurre es integral varias veces la desigualdad conocida 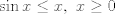 para obtener que para obtener que 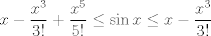 y determinar el limite por la derecha mediante sandwich. mientras que por la izquierda lo determinas por analogia y determinar el limite por la derecha mediante sandwich. mientras que por la izquierda lo determinas por analogia 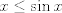 si si 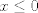 . .Saludos Claudio -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 Oct 30 2017, 03:45 PM Oct 30 2017, 03:45 PM
Publicado:
#3
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 124 Registrado: 29-September 17 Miembro Nº: 153.951 Nacionalidad:  Sexo:  |
? cual es la necesidad de ocupar lhopital ? si el x tiende a 1 no tienes ninguna indeterminación , puedes evaluar directamente.
Creo que tipeaste mal y deberia ser un 0 , si es así el valor es conocido . Prueba multiplicando por algo conveniente para ocupar 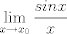
Mensaje modificado por Ignacio.21 el Oct 30 2017, 03:50 PM |
|
|
|
 Oct 30 2017, 08:32 PM Oct 30 2017, 08:32 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 947 Registrado: 28-September 07 Desde: Santiago Miembro Nº: 10.639 Nacionalidad:  Universidad:  Sexo:  |
Hola les traigo este ejercicio, porque no veo una forma de sacar el limite sin l'hopital. ![TEX: \[\mathop {\lim }\limits_{x \to 1} \frac{{x - senx}}{{{x^3}}}\]](/tex-image/39ca6144d83e3f1b273021c35713b0bc.png) Claramente hubo error de tipeo. El límite tiende a 0 en lugar de 1. Podrías usar infinitesimales en el origen. Mensaje modificado por Laðeralus el Oct 30 2017, 08:34 PM |
|
|
|
 Jun 15 2018, 04:25 PM Jun 15 2018, 04:25 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.875 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
.... si es así el valor es conocido . Prueba multiplicando por algo conveniente para ocupar 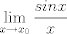 No es tan simple. he visto varias opciones sin L'hopital como utilizar x=3y para obtener de nuevo el limite, lo cual implica demostrar que dicho limite existe. Lo digo porque lo intenté. Saludos Claudio. -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 Jun 15 2018, 05:34 PM Jun 15 2018, 05:34 PM
Publicado:
#6
|
|
|
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 27 Registrado: 17-May 14 Miembro Nº: 129.579 Sexo:  |
La manera clásica es haciendo una expanción de Taylor en 0. Recuerden que
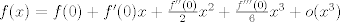 donde 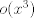 denota una función en denota una función en  tal que tal que 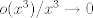 cuando cuando 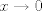 . Tomando . Tomando 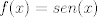 tenemos tenemos 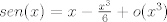 de donde de donde 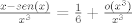 . .
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 05:56 PM |