Licenciatura en matemáticas UCH vs PUC Opciones

[EderC]

Quisiera corregir o comentar algunos de los puntos mencionados por NSHM.

Sobre los electivos, los electivos que menciona son los electivos especializados, los electivos básicos cada año son sólo dos "Creatividad matemática" y algún otro que se dicte que algún profe ofrezca (en mi caso, me dejaron contar el curso que tomé en el IMPA). Y los "electivos especializados" que aparecen en la malla no son "electivos" en sí tampoco: son ramos obligatorios a ser administrados al gusto del alumno, esa fue la idea de ese cambio de malla (fuente: conversación con Behn en su momento y Arenas también).

Lo que sí, puedes hacer electivos a tu gusto (cosa que se puede hacer en todas las Ues imagino ya que en la puc, la usach, la pucv, la usm y la uv se puede). En mi caso hice los siguientes:

• Geometría hiperbólica: con el profesor Antonio Behn, en su oficina semanalmente iba a comentarle mis avances. La evaluación final se basó en hacer una exposición introductoria a la gente de la carrera. Ojo que no está en la malla, fui yo el que se interesó y se acercó al profesor.
  
• Combinatoria: con el profesor José Soto del DIM y en el DIM... aunque lo dejé por los topes de horarios y viajes que a esa hora en Santiago a mi me terminaron por desgastar. Excelentes clases, por cierto. José Soto no tuvo ningún problema en recibirme y el jefe de carrera de entonces no tuvo tampoco drama en aceptarme la solicitud... sólo fallaron en secretaría que nunca entendí bien qué sucedió con la solicitud (¿se perdió?). ¿Cómo supe que él lo dictaría? por u-campus puedes consultar todos los cursos que van a dictarse en todas las facultad de la universidad (así mismo pude tomar ramos en filosofía y en el depto de literatura).
  
• Sistema dinámicos: nunca pudimos empezarlo, pero el ramo iba a dictármelo la profesora Verónica Poblete.
  
• Microeconomía I : no pude tomarlo al final por tope de horario pero el profesor del ramo en FEN me había animado a tomarlo en el magister dado mi interés por aprender Teoría de juegos.

La conclusión: si eres movido al final puedes fabricarte una malla interesante a ti mismo.

Sobre lineal: el álgebra lineal es como la columna vertebral de las matemáticas, y es el lenguaje básico para entrar en las Algebras de Lie (la cual tiene su motivación en la física). De todos modos, si ser aplicado o no es bueno o malo ya pasa por gustos de cada uno y si a msn no le satisfacía, supongo que está en su derecho a no tranzar terreno (aunque exigirle aplicaciones a una carrera de matemática pura es como el equivalente a la frase de pedirle peras al olmo)

Sobre primer año: no es cierto que sea lo mismo, al menos por parte de cálculo I donde te hacen directamente leer el Lima y tienes que vértelas con nociones topológicas. Eso también se ve en la PUC, y me parece algo desmesurado jaja.

Al usuario Ignacio.21: no quiero entrar en una pelea con los chicos de la UlS pero creo que una malla de licenciatura en matemáticas que tiene sólo un ramo de álgebra abstracta y que tiene 4 o 5 ramos de física más uno de análisis numérico y DOS de álgebra lineal... debe revisarse. Sobre la PUCV, no me gustan esas dos físicas y tampoco métodos numéricos pero supongo que es otro enfoque y por algo el cuerpo docente (el cual han renovado y que considero buenísimo, sobre todo porque ahora hay harta gente joven contratada desde afuera) de esa institución lo mantiene. Sobre la UdeC sé poco, pero si después de tantos años todavía hay espacio para Julio Fmat ahí... (es una broma). En todo caso la dualidad Pasten/JulioFmat es como el "yin yang".

Ahora bien, estas Ues tienen un punto a favor que ni la UCh ni la PUC tienen... calidad de vida en sus ciudades, y viejo ¡cuánto pesa poder ver o no el mar, o que el aire fresco entre por los pulmones! acá en Santiago daría lo que fuera porque me cagara encima una gaviota.

Como dije, al final las mallas dan conocimientos formales, lo importante es que uno sea buen alumno (como ya dije: tan facil decirlo, tan difícil hacerlo) aunque sí muchas veces

Mensaje modificado por EderC el Oct 8 2017, 11:12 PM

[Psi]

Como para nhnsn la aplicado es esencial, para mi fue un dolor de cabeza. Entre a Ingenieria primero y deteste cada uno de los ramos. Fisica en la UC tiene las mismas mates que Ingenieria y te puedo decir bien de cerca que no tienen mucho brillo. Yo entendi aplicacion como saber de todo un poquito, pero malito. En Matematicas ves todo 'en profundidad'. Por ejemplo en Calculo II de Mate le dedicamos un mes a la definicion de Integrabilidad(La primera semana fue Ax. del supremo, luego 2 semanas de sumas de Darboux y una de Riemann) lo que en Ingenieria se ve en media clase, justo antes de que te ensenen que es una primitiva.

Mensaje modificado por Psi el Oct 8 2017, 11:37 PM

[Matriu]

Hablaré ahora un poco de los electivos

OPA ("Optativos en Áreas Relacionadas"): Son optativos que (por malla de segundo año, aunque uno puede orrganizar la malla como quiera) son de áreas parecidas a mate. En esta página salen al final. Como experiencia personal, tomé meca i (este curso es para físicos, no para ing) y me costó bastante, pues se supone que para ellos pide edo y cálculo ii, pero yo lo tomé en paralelo con cálculo ii y sin edo, por lo que a veces no entendía bien las edo, ni las integrales de línea (lo tomé en tercer semestre). El cuarto semestre tomé meca ii y fue un curso decente, (aunque la dificultad fue bastante baja comparada con los demás semestres). Lo único que no me gustó de estos cursos, era la "matraca", es decir, derivar como enfermo y que aún así los resultados queden horribles (en fin, mañas mías). Me han dich que también es útil tomar intro a progra, pero progra avanzada tiene fama de ser un ramo muy demandante (de hecho, varios amigos pasaron progra bastante bien, y casi todos botaron progra avanzada XD). Con respecto a los de estadística, ni idea. He oído que algunos compañeros también toman otros ramos de física (cuántica, relatividad), pero no sé si se los cuentan de alguna forma.

OPR ("Optativos de Profundización"): Son cursos que uno elige de una lista que aparece en la página de más arriba. Por lo general sirven para enseñarte lo básico de cada área. Algunos ejemplos que he tomado

Geometría Diferencial Lo tomé en mi quinto semestre (el semestre pasado). El curso se basó en el libro de do Carmo, "Differential Geometry of Curves and Surfaces", que es geometría diferrencial en 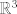. Con respecto al curso, vimos curvas y superficies, hasta el teorema de Gauss-Bonet. Al final también vimos algo de superficies abstractas y mapeo exponencial, pero muy de pasada. La idea del curso siento que se cumplió, con esto me refiero a que ahora puedo tomar un libro de geometría diferencial más avanzado (el de do Carmo, "geometria riemanniana" por ej) y entender algo.

Sistemas Dinámicos Lo estoy tomando ahora. El curso busca dar una introducción a los sistemas dinámicos, definiendo los conceptos de órbita, f invariante, punto atractor, 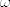límite, entropía, conjugación topológica, dinámica en el círculo, Denjoy, Sharkovsky y gran cantidad de ejemplos (expanding map, el mapeo de Gauss, los fullshift, la herradura de Smale, etc). Actualmente estamos empezando a ver teoría ergódica.

Además, para el otro año pensaba tomar el taller que mencioné en un comentario anterior, geometría algebraica (el libro guía es el "algebraic curves" de William Fulton), por lo general se mandan varias tareas, hay una prueba y el examen es una presentación grupal de algún tópico del Fulton que no se alcanzó a ver en el curso. También me tinca análisis funcional (la dificultad varía n con el profe), donde se ven los teoremas clásicos: Hahn-Banach, Riez, espacios de Hilbert, y no sé que más XD. El otro que tomaría sería teoría de proba, que, es como formalizar las probabilidades usando medida e integración (no diré más porque tampoco se más).

Con respecto a los OPR, hay una regla, el profesor que los dicta debe estar haciendo investigación en el área, es decir, el que hace sistemas dinámicos debe ser dinamista, el que hace geodif debe ser geómetra, etc. Aquí hay un gran pero con el curso de Teoría de Números (es una introducción a la teoría de números, a saber, divisibilidad, módulo, reciprocidad cuadrática, funciones aritméticas o algo de curvas elípticas, según el profe, como libro guía se usa el de Niven, "introduction to theory of numbers"), aquí, la facultad no tiene a nadie haciendo teoría de números, por lo que este curso es hecho por el "profe nuevo" que contratan (2015 geómetra algebraico, 2016 dinamista y físico matemático, 2017 análisis geométrico y edp).

Otra cosa que puedes hacer, es estudiar algún tema con algún profe. Por ejemplo, con unos compañeros estudiamos algo de formas diferenciales con una profesora en nuestro cuarto semestre (usamos "Introduction to Manifolds" de Loring Tu, aunque también vimos algo del "Differential Forms", libro del gran do Carmo jajaja, y por último algo de geometría riemanniana del libro de do Carmo mencionado arriba, pero para ser sincero, entendimos poco y nada de esto último jajaja, lo bueno es que ahora si entendemos algo). Esto fue por amor al arte, es decir, no contaba como ramo, ni como créditos tomados, pero filo, igual se aprendió algo. Ahora también estoy estudiando algo de geo hiperbólica (lo básico) con otro profe. Los métodos de estudio varía bastante según el profe. Con la profe de las formas diferenciales, con mis compañeros nos turnábamos y cada semana, uno presentaba un capítulo del libro de Tu. Con el profe de geo hip, nos juntamos cada dos semanas, estoy leyendo un libro que me prestó él, y cuando nos juntamos le hablo de lo que he leído, o a veces el me da un problema y cuando nos juntamos le presento mi solución (o lo que llevo hasta el momento jajaja) y ahí el me guía un poco, me pregunta y evalúa mi demostración, me dice que cosas puedo mejorar, etc. (esto me ocupa bastante tiempo, no recomiendo hacerlo en un semestre que saber que será pesado, a menos que lo hagas como el taller de iniciación científica).

Otra cosa importante a decir, es la flexibilidad de la malla, uno (teniendo los requisitos) puede tomar los opr, los ofg y los opa cuando a uno se le dé la gana. Una cosa buena es que por lo general, la gente que le va bien avanza más rápido, es decir, toman más cursos por semestre, algunas cosas sin importar los requisitos, etc (aunque si te va mal, es difícil que te den estas libertades nuevamente). También, si te ha ido decente, en cuarto año puedes tomar algún opr de posgrado y puede que te lo cuenten como pregrado. Además, si uno quiere, se puede colar a un curso como oyente, y el profe en la mayoría de los casos no le da color.

Otra cosa, Eder, me podrías dar la bibliografía del curso de geo hiperbólica? XD

Saludos

[pablo gauss]

Quisiera corregir o comentar algunos de los puntos mencionados por NSHM.

Sobre los electivos, los electivos que menciona son los electivos especializados, los electivos básicos cada año son sólo dos "Creatividad matemática" y algún otro que se dicte que algún profe ofrezca (en mi caso, me dejaron contar el curso que tomé en el IMPA). Y los "electivos especializados" que aparecen en la malla no son "electivos" en sí tampoco: son ramos obligatorios a ser administrados al gusto del alumno, esa fue la idea de ese cambio de malla (fuente: conversación con Behn en su momento y Arenas también).

Lo que sí, puedes hacer electivos a tu gusto (cosa que se puede hacer en todas las Ues imagino ya que en la puc, la usach, la pucv, la usm y la uv se puede). En mi caso hice los siguientes:

• Geometría hiperbólica: con el profesor Antonio Behn, en su oficina semanalmente iba a comentarle mis avances. La evaluación final se basó en hacer una exposición introductoria a la gente de la carrera. Ojo que no está en la malla, fui yo el que se interesó y se acercó al profesor.
  
• Combinatoria: con el profesor José Soto del DIM y en el DIM... aunque lo dejé por los topes de horarios y viajes que a esa hora en Santiago a mi me terminaron por desgastar. Excelentes clases, por cierto. José Soto no tuvo ningún problema en recibirme y el jefe de carrera de entonces no tuvo tampoco drama en aceptarme la solicitud... sólo fallaron en secretaría que nunca entendí bien qué sucedió con la solicitud (¿se perdió?). ¿Cómo supe que él lo dictaría? por u-campus puedes consultar todos los cursos que van a dictarse en todas las facultad de la universidad (así mismo pude tomar ramos en filosofía y en el depto de literatura).
  
• Sistema dinámicos: nunca pudimos empezarlo, pero el ramo iba a dictármelo la profesora Verónica Poblete.
  
• Microeconomía I : no pude tomarlo al final por tope de horario pero el profesor del ramo en FEN me había animado a tomarlo en el magister dado mi interés por aprender Teoría de juegos.

La conclusión: si eres movido al final puedes fabricarte una malla interesante a ti mismo.

Sobre lineal: el álgebra lineal es como la columna vertebral de las matemáticas, y es el lenguaje básico para entrar en las Algebras de Lie (la cual tiene su motivación en la física). De todos modos, si ser aplicado o no es bueno o malo ya pasa por gustos de cada uno y si a msn no le satisfacía, supongo que está en su derecho a no tranzar terreno (aunque exigirle aplicaciones a una carrera de matemática pura es como el equivalente a la frase de pedirle peras al olmo)

Sobre primer año: no es cierto que sea lo mismo, al menos por parte de cálculo I donde te hacen directamente leer el Lima y tienes que vértelas con nociones topológicas. Eso también se ve en la PUC, y me parece algo desmesurado jaja.

Al usuario Ignacio.21: no quiero entrar en una pelea con los chicos de la UlS pero creo que una malla de licenciatura en matemáticas que tiene sólo un ramo de álgebra abstracta y que tiene 4 o 5 ramos de física más uno de análisis numérico y DOS de álgebra lineal... debe revisarse. Sobre la PUCV, no me gustan esas dos físicas y tampoco métodos numéricos pero supongo que es otro enfoque y por algo el cuerpo docente (el cual han renovado y que considero buenísimo, sobre todo porque ahora hay harta gente joven contratada desde afuera) de esa institución lo mantiene. Sobre la UdeC sé poco, pero si después de tantos años todavía hay espacio para Julio Fmat ahí... (es una broma). En todo caso la dualidad Pasten/JulioFmat es como el "yin yang".

Ahora bien, estas Ues tienen un punto a favor que ni la UCh ni la PUC tienen... calidad de vida en sus ciudades, y viejo ¡cuánto pesa poder ver o no el mar, o que el aire fresco entre por los pulmones! acá en Santiago daría lo que fuera porque me cagara encima una gaviota.

Como dije, al final las mallas dan conocimientos formales, lo importante es que uno sea buen alumno (como ya dije: tan facil decirlo, tan difícil hacerlo) aunque sí muchas veces

jajajajaajjajajajaajajajajajajajajaja lo de la gaviota es notable , pero si eres movido te puede cagar una paloma

[AdolfoH]

Hola, yo estoy en segundo año de lic en mate de la chile, y me encanta <3
Me gustaria recalcar el tema del ambiente, pero antes es importante mencionar que si bien entramos pocos, tenemos una carrera hermana, la lic en fisica, con la cual tenemos la mayoria de los ramos de formacion básica en comun xd Esto es pulento si a uno le gusta la fisica, porque los ramos de meca I y II están pensados para formar futuros fisicos y tienen muy bien nivel c: Como somos poquitos, uno conoce a la mayoria de las personas, y existe una sala donde uno puede ir a estudiar c: Varias veces me ha pasado que tengo dudas con algún concepto, o problemas con un ejercicio, o simplemente curiosidad con algun area de la matematica que me parece interesante y me han ayudado gente de cursos mayores, desde pregrado a postgrado, y de la misma forma yo ayudo a mis compañeros o a los mechones cuando lo necesitan . Es muy fraternal XD
Si tienes cualquier duda, o te gustaria venir a conocer la carrera, mandame un mensaje c:

[vocin]

Vengo a complementar el comentario del muchacho simpático de arriba con los OPR que he tomado yo

(*) Teoría de números (lo estoy haciendo ahora, 4to semestre). Es un ramo entretenido, hemos visto hasta ahora congruencias, divisibilidad, reciprocidad, orden-raíces primitivas, formas cuadráticas binarias, recurrencias, funciones multiplicativas y vamos ahora en fracciones continuas. El ramo ha tenido tareas cada dos semanas aprox, y el profe es muy motivado. Es entretenido, y al menos el enfoque actual tiene sabor a teoría de números.

(*) Introducción a la Geometría Algebraica (lo hice el semestre pasado, 3er semestre). Se estudia el libro "Algebraic Curves" de William Fulton, y cuando lo hice vimos aprox los primeros 6 caps, y algo del 7mo (Blowup en A^2, que si no me equivoco es el 7.1). El curso está orientado para "gente grande" (cuando lo tomé, estaba yo de 2do, un buen muchacho de 3ro, y el resto eran de 4to+), por lo que el formato fue super relax: tareas para la casa (como 7), una prueba, examen para la casa y presentaciones. Las clases iban a buen ritmo, y como eramos pocos el profe adecuaba el ritmo según íbamos hinchando. Al final del curso nosotros mismos hacíamos las clases (yo expuse un capítulo de aplicaciones a geometría clásica, por ej), así que fue muuuuy ilustrativo. En la prueba nos tuvieron 4 horas y fue masacre jajajjaa.

Las presentaciones podían ser de muuchos temas: capítulos que quedaron colgando del libro, cosas locas, etc... Cito textual

"Como he mencionado en clase varias veces, sugeriría que los estudiantes formen grupos de 2 a 4 personas para la presentación final. Para temas, sugeriría uno de los siguientes:
1. Resolución de singularidades de curvas (vease capítulo 7 de Fulton).
2. El teorema de Riemann.
3. El teorema de Riemann-Roch (véase el capítulo 8 para los puntos 2, 3).
4. Teorema de Mordell para curvas elípticas (véase el libro de Silverman y Tate)
5. Criptografía de curva elíptica
6. Códigos de corrección de errores de geometría algebraica (véase el libro de Judy Walker).

Cualquier otro tema apropiado está muy bien también; en caso de duda, confirme conmigo."

En mi curso, hubo tres grupos: uno habló de cripografía de curvas elípticas, otro de Riemman-Roch y el mío que habló del Teorema de Mordell. Fue muuuy entretenido, y estuvimos infinitas horas en eso jajajja. Un curso muy entretenido para tomar.

[Lichiel]

Porfa no lo hagan. No se metan a esta *** !!!!!
¡Saludos!

[EderC]

existe una sala donde uno puede ir a estudiar c:

Nunca había visto tanta falsedad en una frase

[Gastón Burrull]

Me han dich que también es útil tomar intro a progra

de verdad que no puedo creer que intro a la progra no sea obligatorio, deberían cambiar eso onda ahora

[Legition Rompedi...]

Porfa no lo hagan. No se metan a esta *** !!!!!
¡Saludos!

JAJAJA por eso me arranco de civil mate/licenciatura