Identificarse Registrarse

Psu
Enseñanza Básica
Enseñanza Media
Universidad
Olimpiadas
Comunidad



 
 Reply to this topicStart new topic
> Demostración matrices
Apolodoro95
mensaje Aug 14 2017, 10:53 AM
Publicado: #1


Principiante Matemático
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 5
Registrado: 27-May 16
Miembro Nº: 145.935
Nacionalidad:
Colegio/Liceo: Instituto de Humanidades Luis Campino-1
Universidad: Universidad de Chile-Facultad de Ciencias
Sexo:



Hola,
Tengo un ejercicio en el cual me dan como datos que se tiene D una matriz diagonal (d1...dn) y M que pertenece a la misma matriz de D. Me piden que pruebe que si MD=DM, entonces M es diagonal.

No tengo idea de cómo empezar el ejercicio :cc.
Go to the top of the page
 
+Quote Post
sebaxz18
mensaje Aug 14 2017, 03:33 PM
Publicado: #2


Principiante Matemático Destacado
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 25
Registrado: 6-November 13
Miembro Nº: 124.160
Nacionalidad:
Universidad: Universidad Catolica de Chile-Facultad de Ingenieria
Sexo:



CITA(Apolodoro95 @ Aug 14 2017, 10:53 AM) *
Hola,
M que pertenece a la misma matriz de D.

me imagino que te refieres a que pertenecen al mismo espacio de matrices. Ahora bien lo que yo haria seria tomar el caso en que todos los d de la matriz D son distintos de 0. En ese caso se tiene que existe la inversa de D y se obtiene la igualdad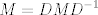
TEX: <br /><br />\begin{equation*}<br />M=DMD^{-1}<br />\end{equation*}<br />

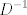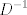En donde se multiplico la igualdad por la derecha por TEX: \begin{equation*}<br />D^{-1}<br />\end{equation*}<br />, ahora bien el lado derecho de la igualdad es una multiplicación de 3 matrices donde

TEX: <br />M=<br />$<br />\begin{bmatrix}<br />m_{11} & m_{12} & . & . & . & m_{1n} \\<br />m_{21} & m_{22} & . & . & . & m_{2n} \\<br />. & . & . & . & . & . \\<br />m_{n1} & m_{n2} & . & . & . & m_{nn} \\ \\<br />\end{bmatrix}<br />$<br />
, es decir una matriz M cualquiera


TEX: <br />D=<br />$<br />\begin{bmatrix}<br />d1 & 0 & . & . & . & 0 \\<br />0 & d2 & . & . & . & 0 \\<br />. & . & . & . & . & . \\<br />0 & 0 & . & . & . & dn \\<br />\end{bmatrix}<br />$<br />
y TEX: \begin{equation*}<br />D^{-1}<br />\end{equation*}<br /> Es una matriz tal que cada elemento de la diagonal es el inverso del correspondiente elemento de la Matriz D.
Finalmente realiza la multiplicación de esas 3 matrices y te das cuenta de que M es diagonal.
Go to the top of the page
 
+Quote Post
Kaissa
mensaje Aug 14 2017, 09:24 PM
Publicado: #3


Dios Matemático Supremo
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 9.897
Registrado: 6-April 08
Miembro Nº: 19.238
Nacionalidad:
Colegio/Liceo: Colegio Villa Maria
Sexo:



CITA(Apolodoro95 @ Aug 14 2017, 10:53 AM) *
Hola,
Tengo un ejercicio en el cual me dan como datos que se tiene D una matriz diagonal (d1...dn) y M que pertenece a la misma matriz de D. Me piden que pruebe que si MD=DM, entonces M es diagonal.

No tengo idea de cómo empezar el ejercicio :cc.



Inducción sobre el tamaño de tu matriz wink.gif


--------------------
Go to the top of the page
 
+Quote Post
 

Reply to this topicStart new topic
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):

 

Versión Lo-Fi Fecha y Hora actual: 4th April 2025 - 10:20 AM
Powered By IP.Board 2.2.1 © 2007  IPS, Inc.