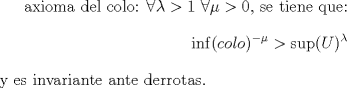|
|
|
|
|
|
|
  |
 Aug 3 2017, 08:24 PM Aug 3 2017, 08:24 PM
Publicado:
#1
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 128 Registrado: 27-November 15 Miembro Nº: 142.558 |
Encuentre todos los triangulos pitagóricos con area un cuadrado perfecto.
|
|
|
|
 Aug 5 2017, 09:36 PM Aug 5 2017, 09:36 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.566 Registrado: 20-June 11 Desde: Region del Maule Miembro Nº: 90.738 Sexo:  |
-------------------- Actualmente en Ingenieria Industrial y en 3er año Ingeniería Civil Mecánica.
From my personal life: I highly recommend this video Click Here! Es altamente deseable tener aptitud para la quimica(termodinámica), la programación, alta comprensión de un problema y planteamiento del mismo, y tener resiliencia al estudiar Ingenieria Civil Industrial. Civil Industrial es en gran parte saber levantar(modelar problemas) procesos logísticos. Puedo dar fe que la Universidad Nacional Andres Bello está adelante de varias U'es Regionales(Calidad similar a la UTAL). Realidad universidades del mundo (18:30): Youtube Quiten Filosofia, Musica y Religión del Curriculum de la Media!! No es recomendado trabajar/colaborar entre matemáticos en general. En general, y a menos que Chile gaste mínimo 2% PIB en I+D, quedarse a investigar en el país, es matarse académicamente. Como recomendación Brasil es un pais muy adelantado en investigación versus AL. Gasto 2023: 0,34%.  |
|
|
|
 Aug 6 2017, 02:57 AM Aug 6 2017, 02:57 AM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.879 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
Encuentre todos los triangulos pitagóricos con area un cuadrado perfecto. Tomemos el post de legition acerca de generar ternas pitagoricas: sin perdida de generalidad, si m y n son coprimos entonces 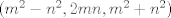 es terna pitagorica y el area es A=mn(m-n)(m+n). Luego es facil deducir que no hay triangulos pitagoricos pues de lo anterior, si lo fuese, debiese ser divisible por m^2 y n^2, es decir, A/mn tendria que ser divisible por m y n, lo que implicaria que el producto (m-n)(m+n) tendria que ser divisible por n y m lo cual es contradiccion pues m-n y m+n no son divisibles por esos numeros. Luego no existe triangulo pitagórico con area igual a un cuadrado perfecto. es terna pitagorica y el area es A=mn(m-n)(m+n). Luego es facil deducir que no hay triangulos pitagoricos pues de lo anterior, si lo fuese, debiese ser divisible por m^2 y n^2, es decir, A/mn tendria que ser divisible por m y n, lo que implicaria que el producto (m-n)(m+n) tendria que ser divisible por n y m lo cual es contradiccion pues m-n y m+n no son divisibles por esos numeros. Luego no existe triangulo pitagórico con area igual a un cuadrado perfecto.Saludos CLaudio -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 Aug 6 2017, 10:37 AM Aug 6 2017, 10:37 AM
Publicado:
#4
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 128 Registrado: 27-November 15 Miembro Nº: 142.558 |
Tomemos el post de legition acerca de generar ternas pitagoricas: sin perdida de generalidad, si m y n son coprimos entonces 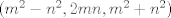 es terna pitagorica y el area es A=mn(m-n)(m+n). Luego es facil deducir que no hay triangulos pitagoricos pues de lo anterior, si lo fuese, debiese ser divisible por m^2 y n^2, es decir, A/mn tendria que ser divisible por m y n, lo que implicaria que el producto (m-n)(m+n) tendria que ser divisible por n y m lo cual es contradiccion pues m-n y m+n no son divisibles por esos numeros. Luego no existe triangulo pitagórico con area igual a un cuadrado perfecto. es terna pitagorica y el area es A=mn(m-n)(m+n). Luego es facil deducir que no hay triangulos pitagoricos pues de lo anterior, si lo fuese, debiese ser divisible por m^2 y n^2, es decir, A/mn tendria que ser divisible por m y n, lo que implicaria que el producto (m-n)(m+n) tendria que ser divisible por n y m lo cual es contradiccion pues m-n y m+n no son divisibles por esos numeros. Luego no existe triangulo pitagórico con area igual a un cuadrado perfecto.Saludos CLaudio Por que deduces que debe ser divisible por $n^2$ y $m^2$? |
|
|
|
 Aug 6 2017, 12:50 PM Aug 6 2017, 12:50 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.566 Registrado: 20-June 11 Desde: Region del Maule Miembro Nº: 90.738 Sexo:  |
.
Mensaje modificado por Legition Rompediskoteqa el Aug 19 2017, 08:42 PM -------------------- Actualmente en Ingenieria Industrial y en 3er año Ingeniería Civil Mecánica.
From my personal life: I highly recommend this video Click Here! Es altamente deseable tener aptitud para la quimica(termodinámica), la programación, alta comprensión de un problema y planteamiento del mismo, y tener resiliencia al estudiar Ingenieria Civil Industrial. Civil Industrial es en gran parte saber levantar(modelar problemas) procesos logísticos. Puedo dar fe que la Universidad Nacional Andres Bello está adelante de varias U'es Regionales(Calidad similar a la UTAL). Realidad universidades del mundo (18:30): Youtube Quiten Filosofia, Musica y Religión del Curriculum de la Media!! No es recomendado trabajar/colaborar entre matemáticos en general. En general, y a menos que Chile gaste mínimo 2% PIB en I+D, quedarse a investigar en el país, es matarse académicamente. Como recomendación Brasil es un pais muy adelantado en investigación versus AL. Gasto 2023: 0,34%.  |
|
|
|
 Aug 6 2017, 01:01 PM Aug 6 2017, 01:01 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 648 Registrado: 26-October 13 Desde: Tokyo-3 Miembro Nº: 123.749 Nacionalidad:  Sexo:  |
Por que deduces que debe ser divisible por $n^2$ y $m^2$? Probablemente utilizando que m, n son enteros y coprimos. Falta explicitar un detallito, que podemos asumir sin pérdida de generalidad que m y n de hecho son coprimos (creo xDDD) -------------------- Pro Tip: Es siempre recomendable saltarse los posts de Insanee/Legition I wish, that I could turn back time 'cos now the guilt is all mine can't live without the trust from those you love I know we can't forget the past you can't forget love & pride because of that, it's killing me inside |
|
|
|
 Aug 6 2017, 01:13 PM Aug 6 2017, 01:13 PM
Publicado:
#7
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 128 Registrado: 27-November 15 Miembro Nº: 142.558 |
Probablemente utilizando que m, n son enteros y coprimos. Falta explicitar un detallito, que podemos asumir sin pérdida de generalidad que m y n de hecho son coprimos (creo xDDD) Caramente eso no vasta, por ejemplo 6^2 = nm claramente es un cuadrado con n = 4, m = 9, n y m son coprimos pero no es divisible por n^2 = 16 ni por m^2 = 81. |
|
|
|
 Aug 6 2017, 01:54 PM Aug 6 2017, 01:54 PM
Publicado:
#8
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |

-------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Aug 6 2017, 02:08 PM Aug 6 2017, 02:08 PM
Publicado:
#9
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |

-------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Aug 6 2017, 04:24 PM Aug 6 2017, 04:24 PM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 648 Registrado: 26-October 13 Desde: Tokyo-3 Miembro Nº: 123.749 Nacionalidad:  Sexo:  |
Caramente eso no vasta, por ejemplo 6^2 = nm claramente es un cuadrado con n = 4, m = 9, n y m son coprimos pero no es divisible por n^2 = 16 ni por m^2 = 81. Completamente de acuerdo! Se me había ido la posiblidad de que m o n tuvieran algún factor primo al cuadrado o así xDDD. -------------------- Pro Tip: Es siempre recomendable saltarse los posts de Insanee/Legition I wish, that I could turn back time 'cos now the guilt is all mine can't live without the trust from those you love I know we can't forget the past you can't forget love & pride because of that, it's killing me inside |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 04:21 PM |










![TEX: \[\begin{gathered}<br /> {\text{Tomemos dos numeros racionales positivos}}{\text{, }} \hfill \\<br /> \frac{a}{b},\frac{c}{d},{\text{ cuyo producto = k}}{\text{, sumando k a cada racional}} \hfill \\<br /> \frac{a}{b} + k = \frac{{a + bk}}{b},{\text{ }}\frac{c}{d} + k = \frac{{c + dk}}{d},{\text{ ahora se amplifica igualando denominador}} \hfill \\<br /> \frac{{ad + bdk}}{{bd}},{\text{ }}\frac{{cb + dbk}}{{db}},{\text{ ahora se elevan los numeradores al cuadrado}} \hfill \\<br /> {\left( {ad + bdk} \right)^2},{\text{ }}{\left( {cb + dbk} \right)^2},{\text{ entonces la hipotenusa es}} \hfill \\<br /> {{\text{a}}^2}{{\text{d}}^2}{\text{ + 2ab}}{{\text{d}}^2}k + {b^2}{d^2}{k^2} + {c^2}{b^2} + 2c{b^2}dk + {d^2}{b^2}{k^2} = {{\text{a}}^2}{{\text{d}}^2}{\text{ + 2ab}}{{\text{d}}^2}k + 2{b^2}{d^2}{k^2} + {c^2}{b^2} + 2c{b^2}dk \hfill \\<br /> {\text{ahora nos piden que el Area sea un cuadrado perfecto}} \hfill \\<br /> \frac{{{{\left( {ad + bdk} \right)}^2}{{\left( {cb + dbk} \right)}^2}}}{2} = k{'^2} = \frac{{{{\left( {\left( {ad + bdk} \right)\left( {cb + dbk} \right)} \right)}^2}}}{2} = \frac{{{{\left( {\left( {adcb + a{d^2}ck + bdcbk + {b^2}{d^2}k} \right)} \right)}^2}}}{2} \hfill \\ <br />\end{gathered} \]](/tex-image/f411ec9390b1c96705f104af3101f957.png)