Identificarse Registrarse

Psu
Enseñanza Básica
Enseñanza Media
Universidad
Olimpiadas
Comunidad



 
 Reply to this topicStart new topic
> Parejas de enteros
LittleKesha
mensaje Aug 3 2017, 01:20 PM
Publicado: #1


Matemático
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 41
Registrado: 10-April 17
Desde: Italia
Miembro Nº: 150.783
Sexo:



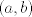Determinar todas la parejas de enteros TEX: $(a,b)$ tales que
TEX: $a^3+b^3+3ab=1$
Go to the top of the page
 
+Quote Post
hermite
mensaje Aug 3 2017, 01:51 PM
Publicado: #2


Maestro Matemático
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 128
Registrado: 27-November 15
Miembro Nº: 142.558
TEX: <br />$$a^3 + b^3 + 3 ab - 1 = 0$$<br />lo que se puede factorizar como<br />$$(a + b - 1)(1 + a + a^2 + b + b^2 - ab) =0$$<br />de aquí tenemos dos posibilidades:<br />$$a + b = 1$$<br />de donde obtenemos las soluciones <br />$$(a, b) = (k, 1- k), k \in \mathbb Z $$<br />y la otra posibilidad es<br />$$(1 + a + a^2 + b + b^2 - ab) =0 $$<br />la que se puede reescribir como<br />$$(a +1)^2 - (a +1)(b +1) + ( b + 1)^2 = 0$$<br />por lo que la única solución en este caso es<br />$$(a,b) = (-1,-1)$$<br />

Mensaje modificado por hermite el Jan 25 2019, 11:19 AM
Go to the top of the page
 
+Quote Post
LittleKesha
mensaje Aug 3 2017, 02:22 PM
Publicado: #3


Matemático
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 41
Registrado: 10-April 17
Desde: Italia
Miembro Nº: 150.783
Sexo:



Muy bien hermite, eres muy fuerte!!! smile.gif
Go to the top of the page
 
+Quote Post
sebitaboom
mensaje Jan 24 2019, 02:40 PM
Publicado: #4


Principiante Matemático
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 5
Registrado: 5-January 19
Miembro Nº: 160.747
Nacionalidad:
Colegio/Liceo: Instituto Alonso de Ercilla
Sexo:



CITA(hermite @ Aug 3 2017, 02:51 PM) *
TEX: <br />$$a^3 + b^3 + 3 ab - 1 = 0$$<br />lo que se puede factorizar como<br />$$(a + b - 1)(1 + a + a^2 + b + b^2 - ab) =0$$<br />de aquí tenemos dos posibilidades:<br />$$a + b = 1$$<br />de donde obtenemos las soluciones <br />$$(a, b) = (k, 1- k), k \in \mathbb Z $$<br />y la otra posibilidad es<br />$$(1 + a + a^2 + b + b^2 - ab) =0 $$<br />la que se puede reescribir como<br />$$(a +1)^2 - (a +1)(b +1) - ( b + 1)^2 = 0$$<br />por lo que la única solución en este caso es<br />$$(a,b) = (-1,-1)$$<br />


no se si ya te diste cuenta, pero hay un error en la ecuacion $$(a+1)^2-(a+1)(b+1)-(b+1)^2$$ y es el hecho que el coeficiente del termino $$(b+1)^2$$ es negativo lo cual al abrir el cuadrado queda un b al cuadradado negativo y mucho mas, pero en lo demas todo ok
Go to the top of the page
 
+Quote Post
sebitaboom
mensaje Jan 24 2019, 02:42 PM
Publicado: #5


Principiante Matemático
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 5
Registrado: 5-January 19
Miembro Nº: 160.747
Nacionalidad:
Colegio/Liceo: Instituto Alonso de Ercilla
Sexo:



CITA(hermite @ Aug 3 2017, 02:51 PM) *
TEX: <br />$$a^3 + b^3 + 3 ab - 1 = 0$$<br />lo que se puede factorizar como<br />$$(a + b - 1)(1 + a + a^2 + b + b^2 - ab) =0$$<br />de aquí tenemos dos posibilidades:<br />$$a + b = 1$$<br />de donde obtenemos las soluciones <br />$$(a, b) = (k, 1- k), k \in \mathbb Z $$<br />y la otra posibilidad es<br />$$(1 + a + a^2 + b + b^2 - ab) =0 $$<br />la que se puede reescribir como<br />$$(a +1)^2 - (a +1)(b +1) - ( b + 1)^2 = 0$$<br />por lo que la única solución en este caso es<br />$$(a,b) = (-1,-1)$$<br />


no se si ya te diste cuenta, pero hay un error en la ecuacion (a+1)^2-(a+1)(b+1)-(b+1)^2 y es el hecho que el coeficiente del termino (b+1)^2 es negativo lo cual al abrir el cuadrado queda un b al cuadradado negativo y mucho mas, pero en lo demas todo ok
Go to the top of the page
 
+Quote Post
hermite
mensaje Jan 25 2019, 11:20 AM
Publicado: #6


Maestro Matemático
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 128
Registrado: 27-November 15
Miembro Nº: 142.558
CITA(sebitaboom @ Jan 24 2019, 02:42 PM) *
no se si ya te diste cuenta, pero hay un error en la ecuacion (a+1)^2-(a+1)(b+1)-(b+1)^2 y es el hecho que el coeficiente del termino (b+1)^2 es negativo lo cual al abrir el cuadrado queda un b al cuadradado negativo y mucho mas, pero en lo demas todo ok

gracias por encontrar el error, era un typo, efectivamente mi intencion fue escribir un signo +.
Go to the top of the page
 
+Quote Post
 

Reply to this topicStart new topic
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):

 

Versión Lo-Fi Fecha y Hora actual: 6th March 2025 - 09:11 PM
Powered By IP.Board 2.2.1 © 2007  IPS, Inc.