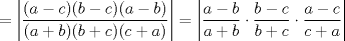|
|
|
|
|
|
|
  |
 Jan 14 2008, 07:46 AM Jan 14 2008, 07:46 AM
Publicado:
#11
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Tenemos otra solución correcta para el problema 2. Creo que no estaba propuesto, así que hay un problema 2' que debiera resultar bastante sencillo (la dificultad radica en que el enunciado no es muy preciso...):
Problema 2': Proponga y demuestre una generalización, considerando n ángulos agudos distintos -------------------- |
|
|
|
 Sep 5 2010, 05:50 PM Sep 5 2010, 05:50 PM
Publicado:
#12
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 61 Registrado: 8-May 10 Miembro Nº: 70.464 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Problema 6:
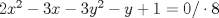  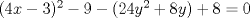 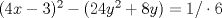 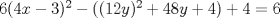 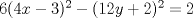 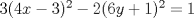 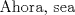 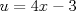 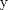 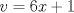 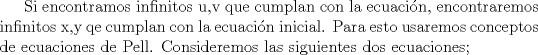 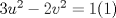 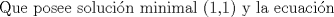 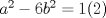 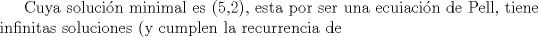 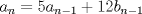 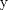 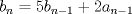  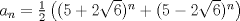 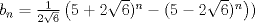 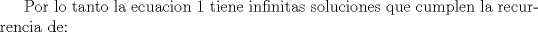 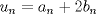 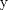 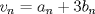 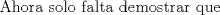 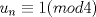 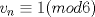 , , 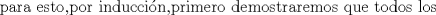 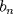 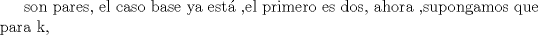 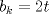 , , 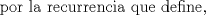 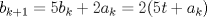 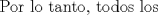 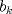 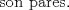 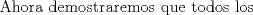 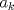 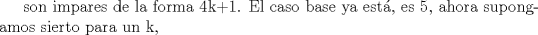  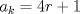 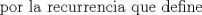 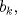 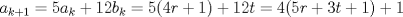 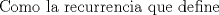 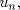 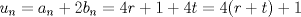 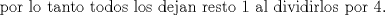 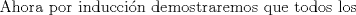 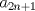 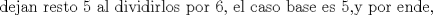 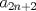 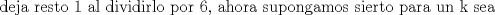 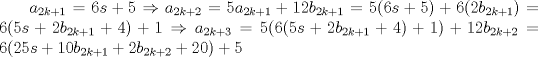 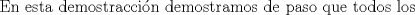 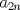 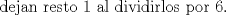 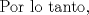 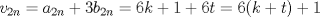 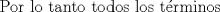 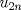 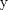 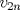 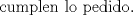 Ahi me salio mati =) Mensaje modificado por Diego Navarro el Sep 7 2010, 03:08 PM |
|
|
|
 Sep 5 2010, 10:22 PM Sep 5 2010, 10:22 PM
Publicado:
#13
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Problema 6: 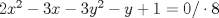  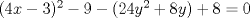 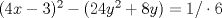 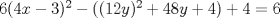 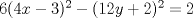 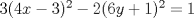 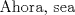 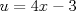 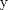 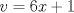 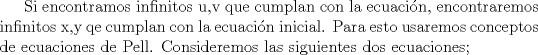 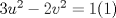 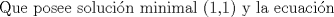 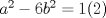 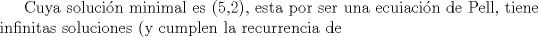 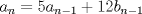 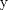 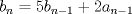 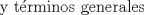 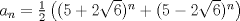 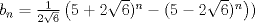 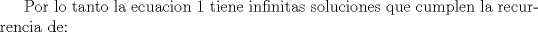  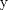 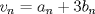 Ahi me salio mati =) Aunque no soy mati... hay un problema: al resolver la ecuación con incógnitas u, v, debes asegurarte que cumplan cierta congruencia mod. 4 y mod. 6, de modo que realmente existan x, y (esto, porque u=4x-3, v=6y+1). Esto quizás nos oblique a despreciar algunas soluciones de la ecuación con incógnitas u, v. -------------------- |
|
|
|
 Sep 7 2010, 03:09 PM Sep 7 2010, 03:09 PM
Publicado:
#14
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 61 Registrado: 8-May 10 Miembro Nº: 70.464 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Gracias por el comentario xsebastian, ahora creo que si
|
|
|
|
 Sep 16 2010, 07:05 PM Sep 16 2010, 07:05 PM
Publicado:
#15
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 61 Registrado: 8-May 10 Miembro Nº: 70.464 Nacionalidad:  Colegio/Liceo:  Sexo:  |
P3:
Primero demostraremos que 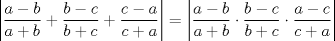 Ahora sin pérdida de generalidad asumamos que 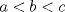 (si fuese isóceles entonces sería cero y a la vez menor que (si fuese isóceles entonces sería cero y a la vez menor que 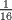 ) entonces existen ) entonces existen 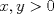 tales que tales que 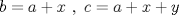 . La desigualdad a demostrar sería; . La desigualdad a demostrar sería;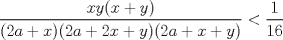 Por desigualdad triangular 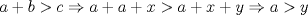 por lo tanto, por lo tanto, 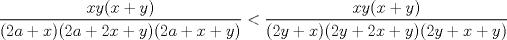 Por otro lado, 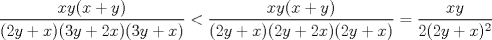 Ahora demostraremos que 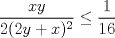 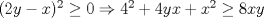 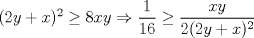
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 18th April 2025 - 10:51 PM |











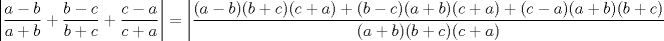
![TEX: $\ =\left|\dfrac{(c+a)[(a-b)(b+c)+(b-c)(a+b)]+(c-a)(a+b)(b+c)}{(a+b)(b+c)(c+a)}\right| $](./tex/7ce93f9556b308b3267e4738674979ff.png)
![TEX: $\ = \left|\dfrac{(c+a)[2ab-2bc]+(c-a)(a+b)(b+c)}{(a+b)(b+c)(c+a)}\right| $](./tex/808b2c607df2f27c6cec1877c14a1392.png)
![TEX: $\ = \left|\dfrac{(a-c)[2bc+2ab]-(a-c)(a+b)(b+c)}{(a+b)(b+c)(c+a)}\right| $](./tex/679258c1ea7310a65a1360b7eca83aee.png)
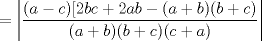
![TEX: $\ = \left|\dfrac{(a-c)[ab+bc-ac-b^2]}{(a+b)(b+c)(c+a)}\right| $](./tex/53a32dcfc879a3ee9e2f71ff3cef72f7.png)