|
|
|
|
|
|
|
  |
 Jun 25 2017, 10:25 PM Jun 25 2017, 10:25 PM
Publicado:
#1
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 9 Registrado: 11-May 17 Miembro Nº: 151.314 Nacionalidad:  Universidad:  Sexo:  |
Muestre que si F un conjunto cerrado contenido en un espacio normal X entonces F es normal.
Si A es conexo contenido en B y B esta contenido en la cerradura de A entonces B es conexo. Ayuda con esos 2 porfa, hice algo pero dudo que este bien. |
|
|
|
 Jun 26 2017, 06:40 PM Jun 26 2017, 06:40 PM
Publicado:
#2
|
|
 Doctor en Matemáticas Grupo: Colaborador Silver Mensajes: 193 Registrado: 17-August 12 Desde: Loncuma :3 Miembro Nº: 110.077 Nacionalidad:  Sexo:  |
|
|
|
|
 Jun 26 2017, 07:24 PM Jun 26 2017, 07:24 PM
Publicado:
#3
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 9 Registrado: 11-May 17 Miembro Nº: 151.314 Nacionalidad:  Universidad:  Sexo:  |
Sabiendo que la clausura de un conexo es conexo, trata de ver ahora como es la clausura de 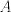 en en 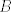 (como subespacio claro). (como subespacio claro).Saludos Esa es mi duda, al hacerlo así no estaría asumiendo lo que quiero demostrar?, por lo que sé, que la clausura de un conexo sea conexo es una consecuencia de lo que puse. Hace poco encontré una forma de hacerlo pero uso una proposición, me gustaría encontrar una forma de hacerlo directo. Saludos Mensaje modificado por Fullton el Jun 26 2017, 07:30 PM |
|
|
|
 Jun 26 2017, 07:40 PM Jun 26 2017, 07:40 PM
Publicado:
#4
|
|
 Doctor en Matemáticas Grupo: Colaborador Silver Mensajes: 193 Registrado: 17-August 12 Desde: Loncuma :3 Miembro Nº: 110.077 Nacionalidad:  Sexo:  |
Esa es mi duda, al hacerlo así no estaría asumiendo lo que quiero demostrar?, por lo que sé, que la clausura de un conexo sea conexo es una consecuencia de lo que puse. Hace poco encontré una forma de hacerlo pero uso una proposición, me gustaría encontrar una forma de hacerlo directo. Saludos Demuestra que la clausura de un conexo es conexo, y de ahí concluye tu problema, es más facil creo (en ese orden). Ahora si andas buscando bibliografia, te recomiendo leer el espacios metricos de E. Lima, con eso nada ha de faltarte <3 shao Mensaje modificado por Niklaash el Jun 26 2017, 07:40 PM |
|
|
|
 Jun 26 2017, 08:00 PM Jun 26 2017, 08:00 PM
Publicado:
#5
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 9 Registrado: 11-May 17 Miembro Nº: 151.314 Nacionalidad:  Universidad:  Sexo:  |
Lo encontré, lo dejaré acá para el que le sirva
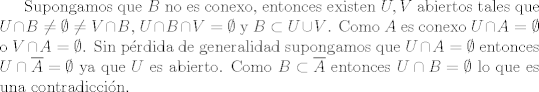 Mensaje modificado por Fullton el Jun 26 2017, 08:15 PM |
|
|
|
 Jul 2 2017, 10:03 AM Jul 2 2017, 10:03 AM
Publicado:
#6
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 98 Registrado: 23-August 13 Miembro Nº: 121.707 Nacionalidad:  Sexo:  |
|
|
|
|
 Jul 2 2017, 04:54 PM Jul 2 2017, 04:54 PM
Publicado:
#7
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 9 Registrado: 11-May 17 Miembro Nº: 151.314 Nacionalidad:  Universidad:  Sexo:  |
|
|
|
|
 Jul 2 2017, 11:02 PM Jul 2 2017, 11:02 PM
Publicado:
#8
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 9 Registrado: 11-May 17 Miembro Nº: 151.314 Nacionalidad:  Universidad:  Sexo:  |
si caché es pa cagarse de la risa jaja el loco amargao al maximo ella xD ----------------------------- encontré el libro ahi va http://math.cankaya.edu.tr/~kenan/Gtopology.pdf Gracias! y no se peleen XD está claro que no es el fin de este foro Saludos |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 05:53 PM |