 Ecuacion simple |
|
|
|
|
|
|
Foro fmat.cl > Sector Preparación PSU - Construyendo tu camino al éxito !! > Banco de Material PSU > Problemas Propuestos Reglamento Sector Propuestos
Para un correcto uso de este foro debes leer estas reglas:
- Los creadores de los temas deben ceñirse a los contenidos PSU.
- Las respuestas deben ir con un desarrollo que explique el resultado final.
- Se prohiben las peleas, descalificaciones y desvirtuar el tema original.
- El creador del tema puede "upear" su tema, después de 5 dias de que lo haya posteado.
- No se permite hacer mas de 3 "up" por tema.
- El titulo del tema debe ser representativo al problema que se posteara.
- Ejemplo: "Ejercicio de Circunferencias, Potencias, Racionalización, etc..."
- Después de que el autor del tema haya quedado satisfecho con las respuestas, debera escribir "resuelto" en el título del tema o en la descripción de la discusión.
Staff FMAT
  |
 Jun 5 2017, 03:45 PM
Publicado:
#1
|
|
|
Dios Matemático Supremo  Grupo: Usuario FMAT Mensajes: 817 Registrado: 21-February 14 Miembro Nº: 127.064  |
Resolver
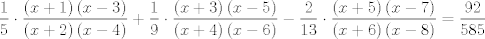 se espera una solucion creativa 
Mensaje modificado por pprimo el Jun 5 2017, 04:40 PM |
 |
 
|
|
Nov 1 2017, 10:35 AM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.566 Registrado: 20-June 11 Desde: Region del Maule Miembro Nº: 90.738 Sexo:  |
Veamos que los terminos son (x-8),(x-7),(x-6),(x-5),(x-4) y (x-3) por el lado de los positivos esta (x+1),(x+2),(x+3),(x+4),(x+5),(x+6). Intuitivamente estos terminos siguen una sucesion de la forma n-k, por lo que es posible generar factoriales de la forma:
![TEX: \[\frac{{n!}}{{\left( {n - r} \right)!}}\]<br />](/tex-image/51d088ef94613639a0a749cfb8122c93.png) Luego debiera quedar algo factorizable y vualá. O la otra forma es ver que la diferencia siempre es de 2 unidades por lo que podriamos sumar 0 y dejar expresada la multiplicación en (x-l)^2-m arriba y abajo. Mensaje modificado por Legition Rompediskoteqa el Nov 1 2017, 11:36 AM -------------------- Actualmente en Ingenieria Industrial y en 3er año Ingeniería Civil Mecánica.
From my personal life: I highly recommend this video Click Here! Es altamente deseable tener aptitud para la quimica(termodinámica), la programación, alta comprensión de un problema y planteamiento del mismo, y tener resiliencia al estudiar Ingenieria Civil Industrial. Civil Industrial es en gran parte saber levantar(modelar problemas) procesos logísticos. Puedo dar fe que la Universidad Nacional Andres Bello está adelante de varias U'es Regionales(Calidad similar a la UTAL). Realidad universidades del mundo (18:30): Youtube Quiten Filosofia, Musica y Religión del Curriculum de la Media!! No es recomendado trabajar/colaborar entre matemáticos en general. En general, y a menos que Chile gaste mínimo 2% PIB en I+D, quedarse a investigar en el país, es matarse académicamente. Como recomendación Brasil es un pais muy adelantado en investigación versus AL. Gasto 2023: 0,34%.  |
|
|
|
|
Dec 26 2017, 02:31 PM
Publicado:
#3
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 50 Registrado: 19-December 17 Miembro Nº: 155.290 |
Note que
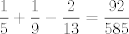
-------------------- La intuición es un arma poderosa en un matemático.-
...Un hermoso cálculo que nació en una noche de inspiración ![TEX: $$\frac{\sqrt[5]{5}}{\sqrt[3]{3}}\cdot \frac{\sqrt[9]{9}}{\sqrt[7]{7}}\cdot \frac{\sqrt[13]{13}}{\sqrt[11]{11}}\cdot \frac{\sqrt[17]{17}}{\sqrt[15]{15}}\cdot \frac{\sqrt[21]{21}}{\sqrt[19]{19}}\cdot \frac{\sqrt[25]{25}}{\sqrt[23]{23}}\cdot ...=\exp \left( -\frac{\pi \gamma }{4}-\frac{\pi }{2}\log 2-\frac{3\pi }{4}\log \pi +\pi \log \Gamma \left( \frac{1}{4} \right) \right)$$](/tex-image/d59471a94884c2506dd649e5016366b1.png) |
|
|
|
|
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 03:05 PM |
