Identificarse Registrarse

Psu
Enseñanza Básica
Enseñanza Media
Universidad
Olimpiadas
Comunidad



 
 Reply to this topicStart new topic
> log(log(log(.)))
pprimo
mensaje May 21 2017, 12:07 AM
Publicado: #1


Dios Matemático Supremo
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 817
Registrado: 21-February 14
Miembro Nº: 127.064
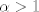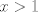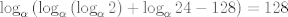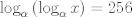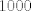
Sea TEX: $$\alpha >1$$ y TEX: $$x>1$$ tales que TEX: $$\log _{\alpha }\left( \log _{\alpha }\left( \log _{\alpha }2 \right)+\log _{\alpha }24-128 \right)=128$$ y TEX: $$\log _{\alpha }\left( \log _{\alpha }x \right)=256$$ Encuentre el resto cuando TEX: $$x$$ es dividido por TEX: $$1000$$
Go to the top of the page
 
+Quote Post
mamboraper
mensaje Jul 28 2017, 02:41 PM
Publicado: #2


Maestro Matemático
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 134
Registrado: 28-March 14
Miembro Nº: 128.100
Nacionalidad:
Sexo:



TEX: Definamos $p=\alpha ^{256}\Rightarrow \sqrt{p}=\alpha ^{128}$, con esto la segunda condición se convierte en $p^p = x^{256}$. Desarrollando la primera condición, se sigue que:\\<br />$\alpha ^{128} = \log_{\alpha}{(\log_{\alpha}{2})}+\log_{\alpha}{24}+\log_{\alpha}{(\frac{1}{\alpha^{128}})}=\log_{\alpha}{(\frac{24\log_{\alpha}{2}}{\alpha^{128}})}\\<br />\alpha^{(\alpha^{128})}=\frac{\log_{\alpha}{2^{24}}}{\alpha^{128}}\Rightarrow \sqrt{p}\alpha^{\sqrt{p}}=\log_{\alpha}{2^{24}}\Rightarrow (\alpha^{\sqrt{p}})^{(\alpha^{\sqrt{p}})}=2^{24}=8^8\Rightarrow \alpha^{\sqrt{p}}=8$\\<br />De esto se sigue que: $\alpha^{\alpha^{128}}=8\Rightarrow (\alpha^{128})^{(\alpha^{128})}=8^{128}=64^{64}\Rightarrow \alpha^{128}=64$\\<br />Luego, $p=64^2=2^{12}\Rightarrow (2^{12})^{(2^{12})}=x^{256}=x^{2^{8}}\Rightarrow 2^{3\cdot 2^{14}}=x^{2^{8}}\Rightarrow 2^{3\cdot 2^{6}}=x$\\<br />Para la siguiente parte, usamos que $2^{10}\equiv 24 \ (\mbox{mod} \ 1000)$. En efecto, $2^{3\cdot 2^2}\equiv 2^{12}\equiv 2^{10}2^2\equiv 24\cdot 4\equiv 2^5\cdot 3 \ (\mbox{mod} \ 1000)$, luego $2^{3\cdot 2^6}\equiv (2^{5}\cdot 3)^{16}\equiv (2^{10})^{8}\cdot 3^{16}\equiv (2^{3}\cdot 3)^{8}\cdot 3^{16}\equiv 2^{24}\cdot 3^{24}\equiv 24\cdot 24\cdot 2^4\cdot 3^{24}\equiv 2^{3}\cdot 3^{27}\equiv (2\cdot 3^{9})^{3}\equiv (458\cdot 27)^{3}\equiv 366^3\equiv 896$ $\blacksquare$


--------------------
Hago clases particulares (activo 2024).
Cualquier consulta por MP.
Go to the top of the page
 
+Quote Post
 

Reply to this topicStart new topic
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):

 

Versión Lo-Fi Fecha y Hora actual: 23rd November 2024 - 07:10 AM
Powered By IP.Board 2.2.1 © 2007  IPS, Inc.