Teorema de Stewart - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Sector Olímpico > Geometría > Teoremas y Formulas

2 Páginas:

1 2 >

Reply to this topic

Start new topic

Teorema de Stewart

「Krizalid」 Ver Perfil del Miembro Ver los mensajes de este miembro	May 28 2007, 03:19 PM Publicado: #1
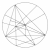
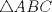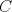Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad: Sexo:	El Teorema de Stewart permite determinar el valor de cualquier ceviana trazada desde uno de los vértices de un triángulo en función de los segmentos determinados por ésta, y los lados de dicho triángulo. Consideremos un $TEX: $\triangle ABC$$ . Por $TEX: $C$$ trazamos una ceviana a la cual denotaremos por "p". Sean m y n los segmentos que determina ésta respectivamente. 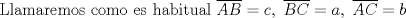$TEX: Llamaremos como es habitual $\overline{AB}=c,\ \overline{BC}=a,\ \overline{AC}=b$$ $TEX: \noindent\underline{Teorema de Stewart}: $c(mn+p^2)=a^2m+b^2n$$ Demostración: 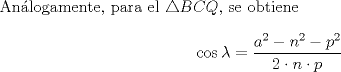$TEX: \noindent Sea $Q$ el punto donde la ceviana toca al lado $\overline{AB}$. De acuerdo con la Ley del coseno para el $\triangle ACQ$, se tiene\\$$\cos\lambda=\frac{m^2+p^2-b^2}{2\cdot m\cdot p}$$$ $TEX: \noindent An\'alogamente, para el $\triangle BCQ$, se obtiene\\$$\cos\lambda=\frac{a^2-n^2-p^2}{2\cdot n\cdot p}$$$ $TEX: \noindent Igualando las dos cantidades obtenidas, se tiene\\\begin{eqnarray}<br /> \frac{{m^2 + p^2 - b^2 }}<br />{m} &=& \frac{{a^2 - n^2 - p^2 }}<br />{n}\\<br /> m^2 n + np^2 - b^2 n &=& a^2 m - mn^2 - mp^2\\<br /> (m^2 n + mn^2 ) + (mp^2 + np^2 ) &=& a^2 m + b^2 n\\<br /> mn(m + n) + p^2 (m + n) &=& a^2 m + b^2 n\\<br /> (m + n)(mn + p^2 ) &=& a^2 m + b^2 n\\<br /> c(mn + p^2 ) &=& a^2 m + b^2 n\ \blacksquare<br />\end{eqnarray}$

Julio_fmat Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 4 2007, 02:58 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 4.874 Registrado: 19-January 07 Desde: Mathematics!! Miembro Nº: 3.830 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Disculpen pero he escuchado el nombre ceviana ya en varias ocaciones, ¿ Cuál es la ceviana ???? Saludos...(un poco desconocido el teorema,aunque mucho más corto que herón...) -------------------- "... Lo veo, pero no puedo creerlo ... se trata de mostrar que las superficies, los volúmenes e incluso las variedades continuas de n dimensiones pueden ponerse en correspondencia unívoca con curvas continuas, o sea, con variedades de una sola dimensión, y que por consiguiente, las superficies, los volúmenes y las variedades de n dimensiones tienen también la misma potencia que las curvas ..." G. Cantor. Las Matemáticas son el lenguaje de la naturaleza, todo lo que nos rodea se puede representar y entender mediante números. Si se hace un gráfico con los números de un sistema, se forman modelos; éstos modelos están por todas partes en la naturaleza. Max Cohen. $TEX: $$\Phi=\displaystyle \int \limits_{-\infty}^x \dfrac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}t^2}dt=\lim_{n\to +\infty}P\left(\dfrac{\displaystyle \sum_{i=1}^n x_i-n\mu}{n\sigma}\le x\right).$$$ Licenciado en Matemática (2021). Universidad de Concepción, Chile.

The Lord Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 4 2007, 06:37 PM Publicado: #3
Dios Matemático Grupo: Usuario FMAT Mensajes: 374 Registrado: 16-September 06 Desde: New Haven, CT, USA. Miembro Nº: 2.275 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Consideremos un triángulo ABC y un punto D tal que pertenesca a la recta BC, en este caso AD es una ceviana. En general se le dice ceviana al segmento que une un vertice con un punto de la recta opuesta a este (siempre considerando al triángulo que estamos observando). Saludos PD(1): No se mencionó "segmento" porque la definición de ceviana abarca tambíen para los puntos que están en la prolongación del segmento. PD(2): A estos trazos se les dice ceviana en honor al matematico italiano Giovanni Ceva, quien es reconocido por su importantisimo Teorema de Ceva.

Julio_fmat Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 4 2007, 07:11 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 4.874 Registrado: 19-January 07 Desde: Mathematics!! Miembro Nº: 3.830 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(The Lord @ Aug 4 2007, 03:37 PM) Consideremos un triángulo ABC y un punto D tal que pertenesca a la recta BC, en este caso AD es una ceviana. En general se le dice ceviana al segmento que une un vertice con un punto de la recta opuesta a este (siempre considerando al triángulo que estamos observando). Saludos PD(1): No se mencionó "segmento" porque la definición de ceviana abarca tambíen para los puntos que están en la prolongación del segmento. PD(2): A estos trazos se les dice ceviana en honor al matematico italiano Giovanni Ceva, quien es reconocido por su importantisimo Teorema de Ceva. Gracias amigo The Lord , se entendería mucho mejor con un dibujito. Saludos. -------------------- "... Lo veo, pero no puedo creerlo ... se trata de mostrar que las superficies, los volúmenes e incluso las variedades continuas de n dimensiones pueden ponerse en correspondencia unívoca con curvas continuas, o sea, con variedades de una sola dimensión, y que por consiguiente, las superficies, los volúmenes y las variedades de n dimensiones tienen también la misma potencia que las curvas ..." G. Cantor. Las Matemáticas son el lenguaje de la naturaleza, todo lo que nos rodea se puede representar y entender mediante números. Si se hace un gráfico con los números de un sistema, se forman modelos; éstos modelos están por todas partes en la naturaleza. Max Cohen. $TEX: $$\Phi=\displaystyle \int \limits_{-\infty}^x \dfrac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}t^2}dt=\lim_{n\to +\infty}P\left(\dfrac{\displaystyle \sum_{i=1}^n x_i-n\mu}{n\sigma}\le x\right).$$$ Licenciado en Matemática (2021). Universidad de Concepción, Chile.

「Krizalid」 Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 4 2007, 07:13 PM Publicado: #5
Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad: Sexo:	Si leíste bien, no habría la necesidad de mostrar un dibujo ya que CITA(The Lord @ Aug 4 2007, 06:37 PM) Consideremos un triángulo ABC y un punto D tal que pertenezca a la recta BC, en este caso AD es una ceviana. donde la explicación es clara.

Julio_fmat Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 4 2007, 07:42 PM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 4.874 Registrado: 19-January 07 Desde: Mathematics!! Miembro Nº: 3.830 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Entonces la ceviana sería algo así como una bisectriz o una altura (claro sin propiedades como se dice vulgarmente).....lo otro existe alguna demostración sin usar trigo....es que la verdad..no me manejo mucho con la ley del coseno y eso... Saludos. -------------------- "... Lo veo, pero no puedo creerlo ... se trata de mostrar que las superficies, los volúmenes e incluso las variedades continuas de n dimensiones pueden ponerse en correspondencia unívoca con curvas continuas, o sea, con variedades de una sola dimensión, y que por consiguiente, las superficies, los volúmenes y las variedades de n dimensiones tienen también la misma potencia que las curvas ..." G. Cantor. Las Matemáticas son el lenguaje de la naturaleza, todo lo que nos rodea se puede representar y entender mediante números. Si se hace un gráfico con los números de un sistema, se forman modelos; éstos modelos están por todas partes en la naturaleza. Max Cohen. $TEX: $$\Phi=\displaystyle \int \limits_{-\infty}^x \dfrac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}t^2}dt=\lim_{n\to +\infty}P\left(\dfrac{\displaystyle \sum_{i=1}^n x_i-n\mu}{n\sigma}\le x\right).$$$ Licenciado en Matemática (2021). Universidad de Concepción, Chile.

laldos Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 5 2007, 07:28 PM Publicado: #7
Principiante Matemático Grupo: Usuario FMAT Mensajes: 3 Registrado: 26-July 07 Miembro Nº: 7.839 Nacionalidad: Sexo:	la ceviana es un segmento q parte de un vertice y corta a su lado opuesto interiormente o exteriorme. se llama ceviana en honor al ingeniero italiano ceva

「Krizalid」 Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 10 2007, 05:41 PM Publicado: #8
Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad: Sexo:	Contenido disponible ahora en Formato de Documento Portátil. Stewart.pdf ( 22.14k ) Número de descargas: 235 Saludos

huentrumanke Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 10 2007, 05:49 PM Publicado: #9
Matemático Grupo: Usuario FMAT Mensajes: 64 Registrado: 20-April 07 Desde: Villarrica Miembro Nº: 5.327 Nacionalidad: Sexo:	No había escuchado acerca de este teorema. La demostración, realmente fácil, elegante, sencilla y entendible en la primera lectura. Saludos.

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 15 2007, 11:21 AM Publicado: #10
Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	CITA(julio @ Aug 4 2007, 07:42 PM) lo otro existe alguna demostración sin usar trigo.... Existe una tal solución, dibujando la altura que parte en el vértice C (observa la figura de Krizalid), escribiendo las tres igualdades que se deducen del teorema de Pitágoras, y "jugando con ellas" (con la intención de obtener expresiones como a²m, b²n, c²p). Sin embargo, las cuentas hacen ver la solución "al estilo de Pitágoras" como si fuese muy "difícil de digerir" (no es de lo más amistosa) Después de todo, el teorema del coseno es una generalización del teorema de Pitágoras. -------------------- Sebastián Elías Puelma Moya Administrador FMAT

« Posterior · Teoremas y Formulas · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 17th April 2025 - 03:32 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.