Libre de triangulos 1 - Foro fmat.cl

Foro fmat.cl > Sector Preparación Olimpiadas > Sector Olímpico > Combinatoria > Problemas Propuestos

Libre de triangulos 1, Teorema de Turán

Opciones

snw Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 5 2017, 02:57 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: Un grafo es una tupla $G=(V,E)$ donde $E\subset \binom{V}{2}$ es el conjunto de arcos, denotaremos por $e(G)=\|E\|$. Un triangulo en $G$ es un trio $a,b,c$ tales que $ab,bc,ac\in E$. Demuestre que si $G$ no tiene triángulos entonces <br />$$e(G)\le \dfrac{n^2}{4}$$$ Hint: Estudie la suma 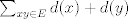$TEX: $\sum_{xy\in E}d(x)+d(y)$$ Mensaje modificado por snw el Apr 5 2017, 02:58 PM -------------------- blep

sushi_8 Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 9 2017, 05:53 PM Publicado: #2
Dios Matemático Grupo: Usuario FMAT Mensajes: 274 Registrado: 20-May 10 Miembro Nº: 71.064 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent Primeramente notemos que dado que $G$ no posee triángulos, para cada arista $xy \in E$ se tendrá que $\text{d}(x) +\text{d}(y) \leq n $, con $n = \# V(G)$. Por lo tanto, $$\sum\limits_{xy \in E} \text{d}(x) +\text{d}(y) \leq n \cdot e(G) $$ <br /><br />\noindent Por otra parte, denotando $N_x$ a los vecinos de $x\in V$, se tiene<br /><br />\begin{align}<br />\sum\limits_{xy \in E} \text{d}(x) +\text{d}(y) &= \sum\limits_{xy \in E} \text{d}(x) +\text{d}(y) \\<br /> &= \dfrac{1}{2}\sum\limits_{x \in V}\sum\limits_{y \in N_x} \text{d}(x) +\text{d}(y) \\<br /> &= \dfrac{1}{2}\sum\limits_{x \in V} \left ( \text{d}(x)^2 + \sum\limits_{y \in N_x} \text{d}(y)\right ) \\<br /> &= \dfrac{1}{2}\sum\limits_{x \in V} \text{d}(x)^2 + \dfrac{1}{2}\sum\limits_{x \in V}\sum\limits_{y \in N_x} \text{d}(y) \\<br /> &= \dfrac{1}{2}\sum\limits_{x \in V} \text{d}(x)^2 + \dfrac{1}{2}\sum\limits_{y \in V}\text{d}(y)\cdot \underbrace{\#\{x \mid y \in N_x \}}_{= \text{d}(y)} \\<br /> &= \sum\limits_{v \in V} \text{d}(v)^2<br />\end{align}<br /><br />\noindent Dado que $f(x) = x^2$ es una función convexa, tomando ponderadores $\lambda_v = \dfrac{1}{n}$ y puntos $x_v = \text{d}(v)$, se obtiene <br /><br />$$ \left ( \dfrac{2e(G)}{n} \right )^2 = f \left ( \sum\limits_{v \in V} \lambda_v x_v \right ) \leq \sum\limits_{v \in V}\lambda_v f(x_v) = \dfrac{1}{n}\sum\limits_{v \in V} \text{d}(v)^2 $$<br /><br />\noindent Juntando las dos desigualdades, obtenemos <br /><br />$$ \left ( \dfrac{2e(G)}{n} \right )^2 \leq e(G) \Longrightarrow e(G)\leq \dfrac{n^2}{4} $$<br />$ -------------------- 100% REAL NO FAKE 1 LINK MEGAUPLOAD KEYGEN + CRACK FULL HD 1080P SUBS ESPAÑOL [PORTABLE]

snw Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 10 2017, 11:56 AM Publicado: #3
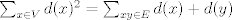Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Perfecto, aunque sólo acotar que podías deducir que $TEX: $\sum_{x\in V}d(x)^2=\sum_{xy\in E}d(x)+d(y)$$ de manera más corta. 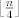Lo otro, es que el ejemplo extremal(cuando se alcanza la cota) es un grafo bipartito donde sus partes tienen tamaño más o menos $TEX: $\lfloor\frac{n}{4}\rfloor$$ . Mensaje modificado por snw el Apr 10 2017, 11:58 AM -------------------- blep

« Posterior · Problemas Propuestos · Anterior »

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 3rd April 2025 - 11:06 PM