|
|
|
|
|
|
|
  |
 May 27 2007, 11:40 PM May 27 2007, 11:40 PM
Publicado:
#1
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Y lejos el nivel mas complejo (distante de la dificultad de los otros) asi que a deleitarse con los problemitas. Esperamos sus soluciones.
Saludos
Archivo(s) Adjunto(s)
-------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 May 28 2007, 07:32 AM May 28 2007, 07:32 AM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo:  Universidad:  Sexo:  |
 No sé si esté bien la solución, se me ocurrió recién, sería una lástima que sí lo estuviera. Ahh creo que está mala porque etsoy asumiendo que 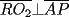 lo cual claramente no siempre es cierto. lo cual claramente no siempre es cierto.
Mensaje modificado por caf_tito el May 28 2007, 06:45 PM -------------------- |
|
|
|
 Jun 27 2007, 04:42 PM Jun 27 2007, 04:42 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
La solución estaría incorrecta... al menos, yo veo el primer error al asumir que
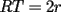 . De cualquier modo, el valor obtenido para . De cualquier modo, el valor obtenido para 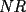 es correcto, es decir: es correcto, es decir: 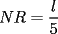 Podemos decir que este problema es la "versión concreta" de una generalización, que he publicado aquí. Por cierto, la idea de resolución es la misma (digamos de algún modo, que la "versión general" es la herramienta para proponer pequeñas variantes del mismo problema) PD: Este problema, me parece haberlo visto antes, en algún lugar... Saludos -------------------- |
|
|
|
 Jun 28 2007, 05:55 PM Jun 28 2007, 05:55 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo:  Universidad:  Sexo:  |
En Todo caso, la justificación de
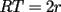 es sencilla (incluso la aprendí xD por ti en una respuesta q diste a unejercicio PSU) pero eso se cumple solo al suponer que RT es Tangente (un pitágoras y listo) pero lamentablemente creo que ahí está el error, como dije en asumir que ese trazo puede ser tangente común a las 2 circunferencias. es sencilla (incluso la aprendí xD por ti en una respuesta q diste a unejercicio PSU) pero eso se cumple solo al suponer que RT es Tangente (un pitágoras y listo) pero lamentablemente creo que ahí está el error, como dije en asumir que ese trazo puede ser tangente común a las 2 circunferencias.
Mensaje modificado por caf_tito el Jun 28 2007, 06:49 PM -------------------- |
|
|
|
 Aug 4 2007, 11:25 AM Aug 4 2007, 11:25 AM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo:  Universidad:  Sexo:  |

Mensaje modificado por caf_tito el Aug 4 2007, 07:22 PM
Archivo(s) Adjunto(s)
-------------------- |
|
|
|
 Aug 7 2007, 10:21 AM Aug 7 2007, 10:21 AM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
La solución es correcta, en cuanto expliques cómo usaste el teorema de Thales, para concluir que el segmento NR mide la quinta parte de l
Lo más difícil eran las construcciones auxiliares, pero la explicación está clara PD: Ya me acordé (revisando el libro de las OBM, 9ª a 16ª), el problema está sacado de una OBM -------------------- |
|
|
|
 Aug 9 2007, 09:08 PM Aug 9 2007, 09:08 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo:  Universidad:  Sexo:  |

-------------------- |
|
|
|
 Aug 10 2007, 08:26 PM Aug 10 2007, 08:26 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Después de todas las intervenciones de caf_tito, este problema 2 tiene solución correcta... falta por resolver el problema 1, espero que salga "por las buenas" (sin tantas cuentas)
PD: La vida en RJ está ajetreada, espero que pronto cuente con más tiempo... -------------------- |
|
|
|
 Nov 13 2011, 02:33 PM Nov 13 2011, 02:33 PM
Publicado:
#9
|
|
|
Matemático Grupo: Validating Mensajes: 50 Registrado: 22-October 11 Desde: Santiago Miembro Nº: 96.078 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Para la P2 me base en los minutos que demoraba para calcular la respuesta, los minutos que demora en ir y volver equivalen al doble del kilómetro que esta pintando la maquina.
En el primer día, sus recorridos (llamaremos recorrido a la ida y vuelta) demoran: 2min,4min,6min,8min,10min,12min,14min,16min,18min, y el ultimo, de 20 min(para pintar el kilometro 10) queda hasta la mitad, es decir, solo lo pinta sin devolverse a rellenar el estanque. luego, para el día 2: 10 min(para devolverse de donde quedo el dia anterior), 22 min, 24 min, 26 min, y el ultimo (kilometro 14), para el cual se necesitan 28 minutos, no es terminado, le faltan 10 minutos ( es decir, lo pinto y avanzo 4 kilometros de vuelta) día 3: 10min(lo que faltaba del dia anterior para rellenar),30min,32min, y el ultimo recorrido quedo casi terminado, le faltaron 6 kilometros para llegar a rellenar. día 4: 6min, 36min, 38 min, y el kilometro 20 quedo pintado y la maquina quedo ahi, es decir, a 20 kilometros del tambor de pintura. dia 5: 20min,42min, y el kilometro 22 quedo pintado y la maquina se encuentra a 6km del tambor. dia 6: 6min, 46min, 48min, aqui queda exactamente en el tambor de pintura. dia 7: 50min, y termina de pintar el kilometro 26 pero le faltan 2 km para llegar nuevamente al tambor. dia 8: 2min, 54min y el kilometro 28 queda pintado, pero la maquina queda a 12km del tambor dia 9: 12 min, 58 min, y el kilometro 30 queda pintado y la maquina se encuentra a 30km del tambor dia 10: 30min, 62 min, es decir, le quedan 8 minutos para terminar su trabajo por el dia, y todavia le faltan 32 km para terminar de pintar el segundo kilometro del dia, por lo tanto, pinta 1 kilometro y queda a 1/4 de camino para terminar el segundo.. La respuesta es el día 10. |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 09:19 PM |














