|
|
|
|
|
|
|
  |
 May 27 2007, 10:41 PM May 27 2007, 10:41 PM
Publicado:
#1
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
Método gráfico
En el proceso de factorizar una inecuación cuadrática nos resultan inecuaciones de la forma 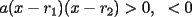 , etc. Con , etc. Con  La solución de esta inecuación también puede hallarse empleando un método gráfico, conocido comúnmente como el método de las cruces o del cementerio. La eficacia de éste método se manifiesta cuado deseamos resolver una inecuación de grado 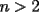 , osea, cuando al factorizar se obtiene una inecuación de la forma , osea, cuando al factorizar se obtiene una inecuación de la forma 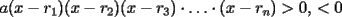 , etc. Con , etc. Con 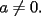 Procedimiento para emplear el método gráfico 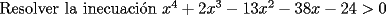 1.- Factorizamos el polinomio  2.- Trazamos una rectal real, ubicando las raíces de la inecuación 3.- En una tabla se escriben verticalmente cada factor, y horizontalmente cada intervalo tomando como referencia la recta real de la siguiente manera: ![TEX: \[<br />\begin{array}{*{20}c}<br /> {} &\vline & { - \infty , - 3} &\vline & { - 3, - 2} &\vline & { - 2, - 1} &\vline & { - 1,4} &\vline & {4,\infty } \\<br />\hline<br /> {x + 1} &\vline & {} &\vline & {} &\vline & {} &\vline & {} &\vline & {} \\<br />\hline<br /> {x + 2} &\vline & {} &\vline & {} &\vline & {} &\vline & {} &\vline & {} \\<br />\hline<br /> {x + 3} &\vline & {} &\vline & {} &\vline & {} &\vline & {} &\vline & {} \\<br />\hline<br /> {x - 4} &\vline & {} &\vline & {} &\vline & {} &\vline & {} &\vline & {} \\<br />\hline<br /> {} &\vline & {} &\vline & {} &\vline & {} &\vline & {} &\vline & {} \\<br /><br /> \end{array} <br />\]](./tex/154045.gif) 4.- Se evalúa cada factor por cada intervalo para así determinar su signo. Para la evaluación se pueden tomar cualesquiera de los valores que pertenezcan al intervalo, con excepción de los valores de los extremos (las raíces que anulan tanto a uno como otro factor). Empleando dicho procedimiento, se obtendrá: ![TEX: \[<br />\begin{array}{*{20}c}<br /> {} &\vline & { - \infty , - 3} &\vline & { - 3, - 2} &\vline & { - 2, - 1} &\vline & { - 1,4} &\vline & {4,\infty } \\<br />\hline<br /> {x + 1} &\vline & - &\vline & - &\vline & - &\vline & + &\vline & + \\<br />\hline<br /> {x + 2} &\vline & - &\vline & - &\vline & + &\vline & + &\vline & + \\<br />\hline<br /> {x + 3} &\vline & - &\vline & + &\vline & + &\vline & + &\vline & + \\<br />\hline<br /> {x - 4} &\vline & - &\vline & - &\vline & - &\vline & - &\vline & + \\<br />\hline<br /> {} &\vline & {} &\vline & {} &\vline & {} &\vline & {} &\vline & {} \\<br /><br /> \end{array} <br />\]](./tex/154046.gif) 5.- Haciendo uso de la Regla de los signos, se multiplican verticalmente los signos obtenidos para obtener el resultado, entonces: ![TEX: \[<br />\begin{array}{*{20}c}<br /> {} &\vline & { - \infty , - 3} &\vline & { - 3, - 2} &\vline & { - 2, - 1} &\vline & { - 1,4} &\vline & {4,\infty } \\<br />\hline<br /> {x + 1} &\vline & - &\vline & - &\vline & - &\vline & + &\vline & + \\<br />\hline<br /> {x + 2} &\vline & - &\vline & - &\vline & + &\vline & + &\vline & + \\<br />\hline<br /> {x + 3} &\vline & - &\vline & + &\vline & + &\vline & + &\vline & + \\<br />\hline<br /> {x - 4} &\vline & - &\vline & - &\vline & - &\vline & - &\vline & + \\<br />\hline<br /> {} &\vline & + &\vline & - &\vline & + &\vline & - &\vline & + \\<br /><br /> \end{array} <br />\]](./tex/154047.gif) 6.- Finalmente, se observa el sentido de la igualdad de la inecuación. Si el sentido de la inecuación es  , la solución estará constituida por la unión de los intervalos, los cuales indiquen el signo "+". En caso contrario, si el sentido de la inecuación es , la solución estará constituida por la unión de los intervalos, los cuales indiquen el signo "+". En caso contrario, si el sentido de la inecuación es  , la solución estará constituída por la unión de los intervalos, los cuales indiquen el signo "-". , la solución estará constituída por la unión de los intervalos, los cuales indiquen el signo "-".La solución de la inecuación será  , ó en notación de intervalos , ó en notación de intervalos 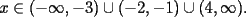 Inecuaciones que contienen fracciones El método expuesto anteriormente se puede extender a la solución de inecuaciones que contienen fracciones algebraicas. Lo primero que debemos hacer es excluir los números reales que anulan a los denominadores. Luego, pasamos todas las fracciones y demás expresiones algebraicas al miembro izquierdo de la desigualdad. El próximo paso consiste en reducir las expresiones algebraicas en el miembro izquierdo a una sola fracción. Por último, después de factorizar tanto el numerador como el denominador aplicamos el método de las cruces, teniendo en cuenta los factores del numerador como los del denominador. Resolver la inecuación 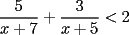 Solución:  (Nótese que al dividir la inecuación por 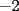 , se cambia el sentido de la desigualdad). , se cambia el sentido de la desigualdad).Aplicando el método gráfico, tendremos: ![TEX: \[<br />\begin{array}{*{20}c}<br /> {} &\vline & { - \infty , - 7} &\vline & { - 7, - 6} &\vline & { - 6, - 5} &\vline & { - 5, - 2} &\vline & { - 2,\infty } \\<br />\hline<br /> {x + 2} &\vline & - &\vline & - &\vline & - &\vline & - &\vline & + \\<br />\hline<br /> {x + 6} &\vline & - &\vline & - &\vline & + &\vline & + &\vline & + \\<br />\hline<br /> {x + 7} &\vline & - &\vline & + &\vline & + &\vline & + &\vline & + \\<br />\hline<br /> {x + 5} &\vline & - &\vline & - &\vline & - &\vline & + &\vline & + \\<br />\hline<br /> {} &\vline & + &\vline & - &\vline & + &\vline & - &\vline & + \\<br /><br /> \end{array} <br />\]](./tex/154055.gif) 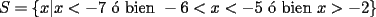 , , 
|
|
|
|
 Jun 14 2007, 01:59 AM Jun 14 2007, 01:59 AM
Publicado:
#2
|
|
|
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 21 Registrado: 13-March 07 Miembro Nº: 4.505 Nacionalidad:  Colegio/Liceo:  Sexo:  |
loko pulento... me tan pasando esto recien... asi ke a darle duro no maa...
|
|
|
|
 Aug 30 2007, 02:46 AM Aug 30 2007, 02:46 AM
Publicado:
#3
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 486 Registrado: 31-October 06 Desde: Cordoba! argentina ,altura de 2,71828182845904523. Miembro Nº: 2.689 Nacionalidad:  Colegio/Liceo:  Sexo:  |
excelente!
como profesor ut un 7 me sirvio mucho tu guia de inecuaciones enserio muchisimas gracias Krizalid -------------------- mi táctica es quedarme en tu recuerdo no sé cómo ni sé con qué pretexto pero quedarme en vos  Y si te queda tiempo duermes...! Estudiante de Ingenieria Civil Universidad Nacional de Cordoba |
|
|
|
 Sep 15 2007, 05:37 PM Sep 15 2007, 05:37 PM
Publicado:
#4
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
|
|
|
|
 Feb 5 2008, 06:03 PM Feb 5 2008, 06:03 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 4.874 Registrado: 19-January 07 Desde: Mathematics!! Miembro Nº: 3.830 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Método gráfico En el proceso de factorizar una inecuación cuadrática nos resultan inecuaciones de la forma 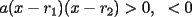 , etc. Con , etc. Con  La solución de esta inecuación también puede hallarse empleando un método gráfico, conocido comúnmente como el método de las cruces o del cementerio. La eficacia de éste método se manifiesta cuado deseamos resolver una inecuación de grado 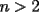 , osea, cuando al factorizar se obtiene una inecuación de la forma , osea, cuando al factorizar se obtiene una inecuación de la forma 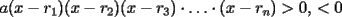 , etc. Con , etc. Con 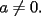 Procedimiento para emplear el método gráfico 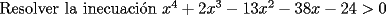 1.- Factorizamos el polinomio  2.- Trazamos una rectal real, ubicando las raíces de la inecuación 3.- En una tabla se escriben verticalmente cada factor, y horizontalmente cada intervalo tomando como referencia la recta real de la siguiente manera: ![TEX: \[<br />\begin{array}{*{20}c}<br /> {} &\vline & { - \infty , - 3} &\vline & { - 3, - 2} &\vline & { - 2, - 1} &\vline & { - 1,4} &\vline & {4,\infty } \\<br />\hline<br /> {x + 1} &\vline & {} &\vline & {} &\vline & {} &\vline & {} &\vline & {} \\<br />\hline<br /> {x + 2} &\vline & {} &\vline & {} &\vline & {} &\vline & {} &\vline & {} \\<br />\hline<br /> {x + 3} &\vline & {} &\vline & {} &\vline & {} &\vline & {} &\vline & {} \\<br />\hline<br /> {x - 4} &\vline & {} &\vline & {} &\vline & {} &\vline & {} &\vline & {} \\<br />\hline<br /> {} &\vline & {} &\vline & {} &\vline & {} &\vline & {} &\vline & {} \\<br /><br /> \end{array} <br />\]](./tex/154045.gif) 4.- Se evalúa cada factor por cada intervalo para así determinar su signo. Para la evaluación se pueden tomar cualesquiera de los valores que pertenezcan al intervalo, con excepción de los valores de los extremos (las raíces que anulan tanto a uno como otro factor). Empleando dicho procedimiento, se obtendrá: ![TEX: \[<br />\begin{array}{*{20}c}<br /> {} &\vline & { - \infty , - 3} &\vline & { - 3, - 2} &\vline & { - 2, - 1} &\vline & { - 1,4} &\vline & {4,\infty } \\<br />\hline<br /> {x + 1} &\vline & - &\vline & - &\vline & - &\vline & + &\vline & + \\<br />\hline<br /> {x + 2} &\vline & - &\vline & - &\vline & + &\vline & + &\vline & + \\<br />\hline<br /> {x + 3} &\vline & - &\vline & + &\vline & + &\vline & + &\vline & + \\<br />\hline<br /> {x - 4} &\vline & - &\vline & - &\vline & - &\vline & - &\vline & + \\<br />\hline<br /> {} &\vline & {} &\vline & {} &\vline & {} &\vline & {} &\vline & {} \\<br /><br /> \end{array} <br />\]](./tex/154046.gif) 5.- Haciendo uso de la Regla de los signos, se multiplican verticalmente los signos obtenidos para obtener el resultado, entonces: ![TEX: \[<br />\begin{array}{*{20}c}<br /> {} &\vline & { - \infty , - 3} &\vline & { - 3, - 2} &\vline & { - 2, - 1} &\vline & { - 1,4} &\vline & {4,\infty } \\<br />\hline<br /> {x + 1} &\vline & - &\vline & - &\vline & - &\vline & + &\vline & + \\<br />\hline<br /> {x + 2} &\vline & - &\vline & - &\vline & + &\vline & + &\vline & + \\<br />\hline<br /> {x + 3} &\vline & - &\vline & + &\vline & + &\vline & + &\vline & + \\<br />\hline<br /> {x - 4} &\vline & - &\vline & - &\vline & - &\vline & - &\vline & + \\<br />\hline<br /> {} &\vline & + &\vline & - &\vline & + &\vline & - &\vline & + \\<br /><br /> \end{array} <br />\]](./tex/154047.gif) 6.- Finalmente, se observa el sentido de la igualdad de la inecuación. Si el sentido de la inecuación es 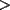 , la solución estará constituida por la unión de los intervalos, los cuales indiquen el signo "+". En caso contrario, si el sentido de la inecuación es , la solución estará constituida por la unión de los intervalos, los cuales indiquen el signo "+". En caso contrario, si el sentido de la inecuación es 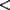 , la solución estará constituída por por la unión de los intervalos, los cuales indiquen el signo "-". , la solución estará constituída por por la unión de los intervalos, los cuales indiquen el signo "-".La solución de la inecuación será  , ó en notación de intervalos , ó en notación de intervalos 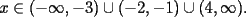 Inecuaciones que contienen fracciones El método expuesto anteriormente se puede extender a la solución de inecuaciones que contienen fracciones algebraicas. Lo primero que debemos hacer es excluir los números reales que anulan a los denominadores. Luego, pasamos todas las fracciones y demás expresiones algebraicas al miembro izquierdo de la desigualdad. El próximo paso consiste en reducir las expresiones algebraicas en el miembro izquierdo a una sola fracción. Por último, después de factorizar tanto el numerador como el denominador aplicamos el método de las cruces, teniendo en cuenta los factores del numerador como los del denominador. Resolver la inecuación 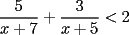 Solución:  (Nótese que al dividir la inecuación por 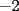 , se cambia el sentido de la desigualdad). , se cambia el sentido de la desigualdad).Aplicando el método gráfico, tendremos: ![TEX: \[<br />\begin{array}{*{20}c}<br /> {} &\vline & { - \infty , - 7} &\vline & { - 7, - 6} &\vline & { - 6, - 5} &\vline & { - 5, - 2} &\vline & { - 2,\infty } \\<br />\hline<br /> {x + 2} &\vline & - &\vline & - &\vline & - &\vline & - &\vline & + \\<br />\hline<br /> {x + 6} &\vline & - &\vline & - &\vline & + &\vline & + &\vline & + \\<br />\hline<br /> {x + 7} &\vline & - &\vline & + &\vline & + &\vline & + &\vline & + \\<br />\hline<br /> {x + 5} &\vline & - &\vline & - &\vline & - &\vline & + &\vline & + \\<br />\hline<br /> {} &\vline & + &\vline & - &\vline & + &\vline & - &\vline & + \\<br /><br /> \end{array} <br />\]](./tex/154055.gif) 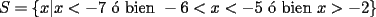 , ,  Tienes un por repetido al igual que en tú PDF. Revisa en la parte donde lo subrayé con rojo. Bueno no sé si será apropiado hacer una consulta del tema aquí ( si no es así lo pueden mover a consultas y tareas), es que tengo una duda con la tabla de los signos positivos y negativos, o sea esto: CODE 4.- Se evalúa cada factor por cada intervalo para así determinar su signo. Para la evaluación se pueden tomar cualesquiera de los valores que pertenezcan al intervalo, con excepción de los valores de los extremos (las raíces que anulan tanto a uno como otro factor). Empleando dicho procedimiento, se obtendrá: ![TEX: \[<br />\begin{array}{*{20}c}<br /> {} &\vline & { - \infty , - 3} &\vline & { - 3, - 2} &\vline & { - 2, - 1} &\vline & { - 1,4} &\vline & {4,\infty } \\<br />\hline<br /> {x + 1} &\vline & - &\vline & - &\vline & - &\vline & + &\vline & + \\<br />\hline<br /> {x + 2} &\vline & - &\vline & - &\vline & + &\vline & + &\vline & + \\<br />\hline<br /> {x + 3} &\vline & - &\vline & + &\vline & + &\vline & + &\vline & + \\<br />\hline<br /> {x - 4} &\vline & - &\vline & - &\vline & - &\vline & - &\vline & + \\<br />\hline<br /> {} &\vline & {} &\vline & {} &\vline & {} &\vline & {} &\vline & {} \\<br /><br /> \end{array} <br />\]](./tex/154046.gif) La consulta es ¿Cómo sabes que signo le corresponde a cada factor? --------------------  "... Lo veo, pero no puedo creerlo ... se trata de mostrar que las superficies, los volúmenes e incluso las variedades continuas de n dimensiones pueden ponerse en correspondencia unívoca con curvas continuas, o sea, con variedades de una sola dimensión, y que por consiguiente, las superficies, los volúmenes y las variedades de n dimensiones tienen también la misma potencia que las curvas ..." G. Cantor. Las Matemáticas son el lenguaje de la naturaleza, todo lo que nos rodea se puede representar y entender mediante números. Si se hace un gráfico con los números de un sistema, se forman modelos; éstos modelos están por todas partes en la naturaleza. Max Cohen.  Licenciado en Matemática (2021). Universidad de Concepción, Chile. |
|
|
|
 Feb 5 2008, 08:03 PM Feb 5 2008, 08:03 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Colaborador Platinum Mensajes: 1.067 Registrado: 11-September 07 Desde: Coquimbo Miembro Nº: 10.097 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
La consulta es ¿Cómo sabes que signo le corresponde a cada factor? Para cada uno de los factores anotados en la primera columna, se reemplaza el valor de "x" por un valor cualquiera dentro del intervalo a considerar. Por ejemplo, y guiándonos con la tabla que ya está. En el factor (x+1) reemplazamos "x" por un valor en ![TEX: $]-\infty, -3[$](./tex/97b6aae072aa09349c64ea1aa4360c87.png) Notemos que por muy pequeño que sea el valor que consideremos dentro de ese intervalo, nunca será mayor que -3, por lo que (x+1) será siempre (dentro de ese intervalo) negativo. Y así sigues haciendo lo mismo con el resto de los intervalos y los otros factores. Espero aclare un poco tu duda, cualquier cosa, pregunta. Saludos. --------------------  "¿Qué es la vida? Una ilusión, una sombra, una ficción, y el mayor bien es pequeño: que toda la vida es sueño, y los sueños, sueños son." |
|
|
|
 Feb 5 2008, 09:58 PM Feb 5 2008, 09:58 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Colaborador Gold Mensajes: 1.374 Registrado: 22-July 06 Desde: San Ramon Miembro Nº: 1.746 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Muy buena guia Krizalid!!!
Es muy útil y clara. Gracias -------------------- Segundo en olimpíadas de Física Región Metropolitana Nivel Tercero Medio, 2006.
Cuarto en olimpíadas de Física Región Metropolitana Nivel Cuarto Medio, 2007. Mejor egresado Instituto Nacional generación 2007 Puntaje Nacional en PSU de Matemáticas 2007, con 850 puntos. Mejor egresado de Ingeniería Civil PUC 2014, con promedio 6,6. |
|
|
|
 Feb 6 2008, 03:25 PM Feb 6 2008, 03:25 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 4.874 Registrado: 19-January 07 Desde: Mathematics!! Miembro Nº: 3.830 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Para cada uno de los factores anotados en la primera columna, se reemplaza el valor de "x" por un valor cualquiera dentro del intervalo a considerar. Por ejemplo, y guiándonos con la tabla que ya está. En el factor (x+1) reemplazamos "x" por un valor en ![TEX: $]-\infty, -3[$](./tex/97b6aae072aa09349c64ea1aa4360c87.png) Notemos que por muy pequeño que sea el valor que consideremos dentro de ese intervalo, nunca será mayor que -3, por lo que (x+1) será siempre (dentro de ese intervalo) negativo. Y así sigues haciendo lo mismo con el resto de los intervalos y los otros factores. Espero aclare un poco tu duda, cualquier cosa, pregunta. Saludos. Bueno ese intervalo corresponde a: ![TEX: $\mathcal{S}$ $= \left\{ {x \in \mathbb{R}\left| {x < - 3} \right.} \right\} = \left] { - \infty , - 3} \right[$](./tex/468859886924bf555eecada7270e5872.png) Pero todavía no entiendo la situación de que al reemplazar por un valor me de negativo. --------------------  "... Lo veo, pero no puedo creerlo ... se trata de mostrar que las superficies, los volúmenes e incluso las variedades continuas de n dimensiones pueden ponerse en correspondencia unívoca con curvas continuas, o sea, con variedades de una sola dimensión, y que por consiguiente, las superficies, los volúmenes y las variedades de n dimensiones tienen también la misma potencia que las curvas ..." G. Cantor. Las Matemáticas son el lenguaje de la naturaleza, todo lo que nos rodea se puede representar y entender mediante números. Si se hace un gráfico con los números de un sistema, se forman modelos; éstos modelos están por todas partes en la naturaleza. Max Cohen.  Licenciado en Matemática (2021). Universidad de Concepción, Chile. |
|
|
|
 Feb 6 2008, 06:31 PM Feb 6 2008, 06:31 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Colaborador Platinum Mensajes: 1.067 Registrado: 11-September 07 Desde: Coquimbo Miembro Nº: 10.097 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Bueno ese intervalo corresponde a: ![TEX: $\mathcal{S}$ $= \left\{ {x \in \mathbb{R}\left| {x < - 3} \right.} \right\} = \left] { - \infty , - 3} \right[$](./tex/468859886924bf555eecada7270e5872.png) Pero todavía no entiendo la situación de que al reemplazar por un valor me de negativo. Toma un valor cualquiera que pertenezca a ese intervalo y reemplazalo por "x" en (x+1) y veamos cuanto te da. Ejemplo: Tomando -5 (que pertenece al intervalo) tenemos: (-5+1)=-4<0 (negativo) Así puedes tomar cualquier otro valor y llegarás a que el factor se vuelve negativo (menor que cero) Saludos. --------------------  "¿Qué es la vida? Una ilusión, una sombra, una ficción, y el mayor bien es pequeño: que toda la vida es sueño, y los sueños, sueños son." |
|
|
|
 Jun 4 2008, 12:48 PM Jun 4 2008, 12:48 PM
Publicado:
#10
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 177 Registrado: 2-August 07 Desde: temuco Miembro Nº: 8.093 Nacionalidad:  Universidad:  Sexo:  |
excelente
-------------------- "Integral Maratón Normal FMAT 2008 - 2009"
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 5th April 2025 - 01:45 AM |