|
|
|
|
|
|
|
  |
 Nov 16 2005, 06:23 PM Nov 16 2005, 06:23 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Vamos con la primera, que no es tan complicada... podría decirse que es la olimpiada iberoamericana más fácil, a medida que pasan los años, la dificultad tiende a aumentar. Pidan ayuda y pongan sus soluciones,
Estén atentos, que a veces podríamos invocar generalizaciones o discutir problemas. 1ª OLIMPIADA IBEROAMERICANA DE MATEMÁTICAS Villa de Leyva, Colombia, 1985 Primera Prueba: Jueves 12 de Diciembre Problema 1: Encuentre todas las ternas 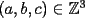 tales que: tales que: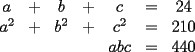 Problema 2: Sea 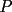 un punto en la región interior del un punto en la región interior del  equilátero, tal que equilátero, tal que 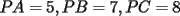 . Determine . Determine  Problema 3: Encuentre las raíces 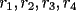 de la ecuación de la ecuación 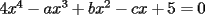 , si se sabe que son reales positivas y que: , si se sabe que son reales positivas y que: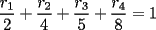 Segunda Prueba: Viernes 13 de Diciembre Problema 4: Sean  tales que tales que  , y : , y :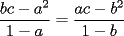 Pruebe que ambas fracciones son iguales a 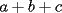 Problema 5: Sea 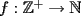 una función que satisface las siguientes condiciones: una función que satisface las siguientes condiciones:
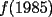 Problema 6: Dado un 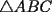 acutángulo sean acutángulo sean 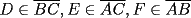 , tales que , tales que 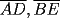 y y 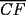 concurren en el circuncentro del triángulo. Si el circunradio mide concurren en el circuncentro del triángulo. Si el circunradio mide  , pruebe que: , pruebe que: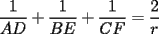 Problemas adicionales (exclusivo para FMAT) Resumen de soluciones -------------------- |
|
|
|
 Nov 16 2005, 09:42 PM Nov 16 2005, 09:42 PM
Publicado:
#2
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 293 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 3 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Solucion al problema 5:
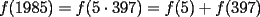 Pero 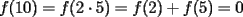 , pero como , pero como 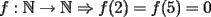 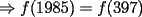 , pero notemos ke , pero notemos ke 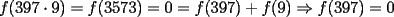 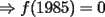 facil y bonito --------------------  |
|
|
|
 Nov 16 2005, 09:47 PM Nov 16 2005, 09:47 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Solución correcta (obviamente
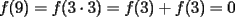 ). Veamos qué tal les va con la siguiente generalización: ). Veamos qué tal les va con la siguiente generalización:Problema 5': Pruebe que 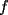 (cumpliendo las condiciones del problema 5) es idénticamente nula, o sea que todo número tiene por imagen a 0 (cumpliendo las condiciones del problema 5) es idénticamente nula, o sea que todo número tiene por imagen a 0
-------------------- |
|
|
|
 Nov 25 2005, 02:03 PM Nov 25 2005, 02:03 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 903 Registrado: 28-May 05 Desde: Santiago, Chile Miembro Nº: 69 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Estoy tratando de hacer el 5'... más rato lo posteo...
Aquí va la solución del 4: 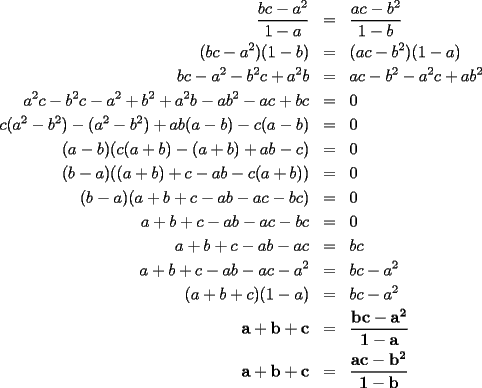 y listo... -------------------- Bachiller en Ciencias
(ex) Estudiante de Medicina Estudiante de Ingeniería Civil de Industrias, diploma en Ingeniería Matemática Pontificia Universidad Católica de Chile  |
|
|
|
 Nov 25 2005, 03:03 PM Nov 25 2005, 03:03 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 903 Registrado: 28-May 05 Desde: Santiago, Chile Miembro Nº: 69 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Solución Problema 1
Como el producto de los tres números es 440, su factorización prima es 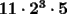 . .Expresado en producto de tres factores, hay estas opciones: 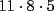 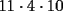 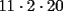 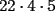 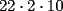 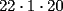 Hay más, pero contienen factores mayores que 24... De estos productos, calculamos la suma de cada uno, siendo 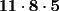 el único con suma 24. el único con suma 24.Ahora sumemos los cuadrados de sus factores: 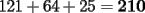 Entonces esta es la única solución, y (obviamente) sus permutaciones: (11,8,5) (11,5,8) (8,11,5) (8,5,11) (5,11,8) (5,8,11) -------------------- Bachiller en Ciencias
(ex) Estudiante de Medicina Estudiante de Ingeniería Civil de Industrias, diploma en Ingeniería Matemática Pontificia Universidad Católica de Chile  |
|
|
|
 Nov 25 2005, 07:56 PM Nov 25 2005, 07:56 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Solución correcta, pero de todos modos creo que es muy sencillo buscar sólo las soluciones enteras... y por un momento perdiste de vista que los enteros incluyen números negativos por allí... ¿Por qué los descartaste?
Sólo daré por hecho el problema, cuando alguien justifique que no pueden aparecer enteros negativos en la solución, o bien si alguien responde el siguiente problema (que es más general): Problema 1': Encuentre todas las soluciones complejas del sistema de ecuaciones del problema 1 -------------------- |
|
|
|
 Nov 25 2005, 08:02 PM Nov 25 2005, 08:02 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
La solución para el problema 4 está impecable, excepto por una cosa que no mencionaste: tenías en un momento:
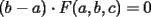 , y concluíste que , y concluíste que 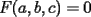 . Eso sucede porque en nuestras hipótesis aparece que . Eso sucede porque en nuestras hipótesis aparece que 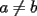 . O sea ese dato que en un principio no se entendía mucho, servía para eso. . O sea ese dato que en un principio no se entendía mucho, servía para eso.-------------------- |
|
|
|
 Dec 11 2005, 11:40 AM Dec 11 2005, 11:40 AM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Aquí una solución para el problema 1, aunque hecho muy a la fuerza y con varias intervenciones. Lo más sano en este caso, es dar una guía con los pasos importantes de la solución:
Primero, como 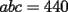 , entonces , entonces 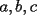 deben ser divisores enteros de 440. Ellos son: deben ser divisores enteros de 440. Ellos son:1 2 4 5 8 10 11 20 22 40 44 55 88 110 220 440 y todos sus inversos aditivos. Segundo, como 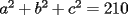 , entonces las posibilidades se reducen a , entonces las posibilidades se reducen a-11 -10 -8 -5 -4 -2 -1 1 2 4 5 8 10 11 Tercero, se eliminan las opciones con números negativos, porque de haber uno, debe haber otro, y entonces no es posible llegar a que 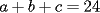 (en realidad queda a+b+c<11) (en realidad queda a+b+c<11)Entonces debo tomar tres números de la lista 1 2 4 5 8 11 admitiendo repeticiones, en principio, para que se cumplan las ecuaciones del sistema. Como 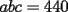 , es necesario elegir 11. Ahora dos números que sumen 13 y multipliquen 40, la única opción que queda es 5 y 8. Por eso la única solución es 5,8,11, y todas las obtenidas por permutaciones. , es necesario elegir 11. Ahora dos números que sumen 13 y multipliquen 40, la única opción que queda es 5 y 8. Por eso la única solución es 5,8,11, y todas las obtenidas por permutaciones.
-------------------- |
|
|
|
 Dec 17 2005, 05:08 PM Dec 17 2005, 05:08 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 903 Registrado: 28-May 05 Desde: Santiago, Chile Miembro Nº: 69 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Solución Problema 3
Si la suma de estos 4 números es 1, su media aritmética es 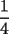 Calculando su media geométrica: ![TEX: $\displaystyle{\sqrt[4]{\frac{r_1\cdot r_2\cdot r_3\cdot r_4}{2\cdot 4\cdot 5\cdot 8}}=\frac{1}{4}}$](./tex/40815.gif) Porque de acuerdo a las fórmulas de Vieta se tiene que: 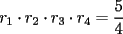 Se sabe que la media aritmética es mayor o igual que la media geométrica, y que la igualdad sólo se cumple cuando los términos involucrados son iguales. Entonces: 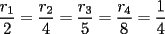 Y las raíces son: 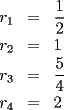 -------------------- Bachiller en Ciencias
(ex) Estudiante de Medicina Estudiante de Ingeniería Civil de Industrias, diploma en Ingeniería Matemática Pontificia Universidad Católica de Chile  |
|
|
|
| Corecrasher |
 Dec 18 2005, 08:56 PM Dec 18 2005, 08:56 PM
Publicado:
#10
|
|
Invitado |
  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img220.imageshack.us/img220/8928/tomapenietenie1es.jpg');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img220.imageshack.us/img220/8928/tomapenietenie1es.jpg');}" /> 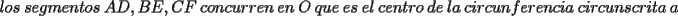 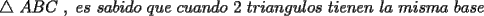 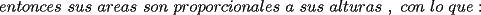  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img516.imageshack.us/img516/8748/triangle2mp.jpg');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img516.imageshack.us/img516/8748/triangle2mp.jpg');}" />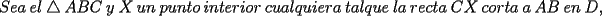 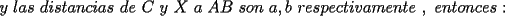 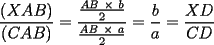
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 18th April 2025 - 06:03 PM |





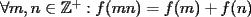
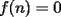 , si la cifra de las unidades de
, si la cifra de las unidades de  es 3
es 3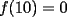
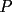 en la región interior de un
en la región interior de un 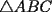 equilátero, con
equilátero, con 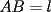 . Supongamos que
. Supongamos que 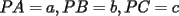 son datos conocidos
son datos conocidos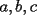
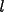 en términos de
en términos de 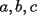
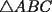 no es acutángulo. Defina los puntos
no es acutángulo. Defina los puntos 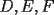 análogamente. Enuncie y demuestre una identidad análoga a la que pide demostrar el problema 6.
análogamente. Enuncie y demuestre una identidad análoga a la que pide demostrar el problema 6.



