|
|
|
|
|
|
|
  |
 Oct 4 2016, 08:57 PM Oct 4 2016, 08:57 PM
Publicado:
#1
|
|
|
Dios Matemático Grupo: Team Ensayos FMAT Mensajes: 274 Registrado: 30-December 09 Miembro Nº: 64.740 Nacionalidad:  Colegio/Liceo:  Sexo:  |
The 33rd. Austrian Mathematical Olympiad OEMO 2002 - Begginer's Competition Problema 1. Calculamos la suma de 7 naturales pares consecutivos (e.g. 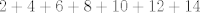 ) y al resultado lo llamaremos ) y al resultado lo llamaremos 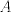 , luego la suma de los siguientes 7 pares consecutivos (en el ejemplo, , luego la suma de los siguientes 7 pares consecutivos (en el ejemplo, 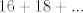 ) y a su resultado llamaremos ) y a su resultado llamaremos 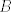 , y finalmente calculamos la suma de los siguientes 7 pares consecutivos y a su resultado llamaremos , y finalmente calculamos la suma de los siguientes 7 pares consecutivos y a su resultado llamaremos 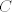 . ¿El producto . ¿El producto 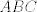 puede resultar puede resultar 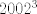 ? ?Problema 2. Pruebe que no existen  tal que x^(floor(x))=9/2. (Disculpen, pero la función floor no aparece y me tira tex error) tal que x^(floor(x))=9/2. (Disculpen, pero la función floor no aparece y me tira tex error)Problema 3. Determine todos los números reales  que satisface la siguiente inecuación que satisface la siguiente inecuación 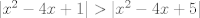 Problema 4. En un trapezoide 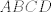 con base con base 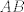 sea sea 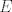 el punto medio del lado el punto medio del lado 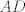 . Supongamos además que . Supongamos además que 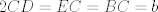 . Sea . Sea 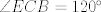 . Construya el trapezoide y determine su área en función de . Construya el trapezoide y determine su área en función de  . .-------------------- He vuelto con las pilas cargaditas!!! |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 6th March 2025 - 10:07 PM |







