|
|
|
|
|
|
|
  |
 Sep 22 2016, 11:23 PM Sep 22 2016, 11:23 PM
Publicado:
#1
|
|
|
Dios Matemático Grupo: Team Ensayos FMAT Mensajes: 274 Registrado: 30-December 09 Miembro Nº: 64.740 Nacionalidad:  Colegio/Liceo:  Sexo:  |
The 33rd. Balkan Mathematical Olympiad Tirana, Albania - 7 de mayo de 2016 Problema 1. Encuentre todas las funciones inyectivas 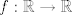 tales que para cada número real tales que para cada número real  y cada entero positivo y cada entero positivo   Problema 2. Sea 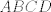 un cuadrilátero cíclico con un cuadrilátero cíclico con 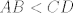 . Las diagonales se intersectan en el punto . Las diagonales se intersectan en el punto 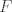 y las rectas y las rectas 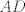 y y 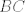 se intersectan en el punto se intersectan en el punto 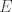 . Sean . Sean 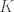 y y 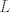 las proyecciones ortogonales de las proyecciones ortogonales de 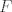 sobre las rectas sobre las rectas 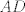 y y 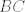 respectivamente, y sean respectivamente, y sean 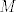 , , 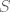 y y 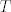 los puntos medios de los puntos medios de 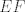 , , 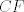 y y 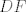 respectivamente. Pruebe que el segundo punto de intersección de las circuncircunferencias de los triángulos respectivamente. Pruebe que el segundo punto de intersección de las circuncircunferencias de los triángulos 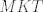 y y 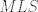 se encuentra en el segmento se encuentra en el segmento 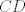 . .Problema 3. Encuentre todos los polinomios mónicos 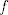 con coeficientes enteros que satisfacen la siguiente condición: Existe un entero positivo con coeficientes enteros que satisfacen la siguiente condición: Existe un entero positivo 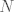 tal que tal que 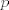 divide a divide a 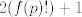 para cada primo para cada primo 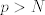 para la cual para la cual 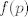 es un entero positivo. es un entero positivo.-------------------- He vuelto con las pilas cargaditas!!! |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 8th July 2025 - 01:23 AM |







