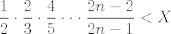|
|
|
|
|
|
|
  |
 Dec 25 2017, 03:10 PM Dec 25 2017, 03:10 PM
Publicado:
#11
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 110 Registrado: 8-February 16 Miembro Nº: 143.585 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
|
|
|
|
 Dec 26 2017, 06:10 AM Dec 26 2017, 06:10 AM
Publicado:
#12
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 50 Registrado: 19-December 17 Miembro Nº: 155.290 |
Cómo puedes comparar X e Y término a término si tienen distinta cantidad de términos? piense cómo -------------------- La intuición es un arma poderosa en un matemático.-
...Un hermoso cálculo que nació en una noche de inspiración ![TEX: $$\frac{\sqrt[5]{5}}{\sqrt[3]{3}}\cdot \frac{\sqrt[9]{9}}{\sqrt[7]{7}}\cdot \frac{\sqrt[13]{13}}{\sqrt[11]{11}}\cdot \frac{\sqrt[17]{17}}{\sqrt[15]{15}}\cdot \frac{\sqrt[21]{21}}{\sqrt[19]{19}}\cdot \frac{\sqrt[25]{25}}{\sqrt[23]{23}}\cdot ...=\exp \left( -\frac{\pi \gamma }{4}-\frac{\pi }{2}\log 2-\frac{3\pi }{4}\log \pi +\pi \log \Gamma \left( \frac{1}{4} \right) \right)$$](/tex-image/d59471a94884c2506dd649e5016366b1.png) |
|
|
|
 Dec 26 2017, 06:20 AM Dec 26 2017, 06:20 AM
Publicado:
#13
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 50 Registrado: 19-December 17 Miembro Nº: 155.290 |
Si, de hecho se puede probar la siguiente desigualdad mas fuerte: 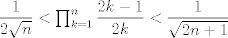 obtengo lo siguiente 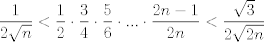 cuando vuelva a stgo publico mi solucion cuando vuelva a stgo publico mi solucion
-------------------- La intuición es un arma poderosa en un matemático.-
...Un hermoso cálculo que nació en una noche de inspiración ![TEX: $$\frac{\sqrt[5]{5}}{\sqrt[3]{3}}\cdot \frac{\sqrt[9]{9}}{\sqrt[7]{7}}\cdot \frac{\sqrt[13]{13}}{\sqrt[11]{11}}\cdot \frac{\sqrt[17]{17}}{\sqrt[15]{15}}\cdot \frac{\sqrt[21]{21}}{\sqrt[19]{19}}\cdot \frac{\sqrt[25]{25}}{\sqrt[23]{23}}\cdot ...=\exp \left( -\frac{\pi \gamma }{4}-\frac{\pi }{2}\log 2-\frac{3\pi }{4}\log \pi +\pi \log \Gamma \left( \frac{1}{4} \right) \right)$$](/tex-image/d59471a94884c2506dd649e5016366b1.png) |
|
|
|
 Dec 26 2017, 06:39 AM Dec 26 2017, 06:39 AM
Publicado:
#14
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 52 Registrado: 5-December 12 Miembro Nº: 114.123 Nacionalidad:  Sexo:  |
|
|
|
|
 Dec 26 2017, 12:19 PM Dec 26 2017, 12:19 PM
Publicado:
#15
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 50 Registrado: 19-December 17 Miembro Nº: 155.290 |
Si, de hecho se puede probar la siguiente desigualdad mas fuerte: 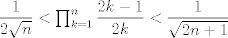 cota inferior, mi demostración es bastante simple pero algo ingeniosa. Designemos por 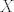 a la cantidad a la cantidad 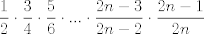 Entonces si elevamos al cuadrado, obtendremos Entonces si elevamos al cuadrado, obtendremos 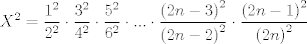 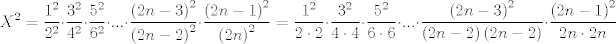 ahora si en el denominador trasladamos un factor a la fracción siguiente nos queda 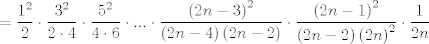 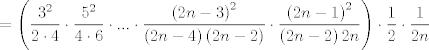 ahora note que la cantidad dentro del parentesis es siempre mayor a 1. el por que queda a su imaginación (es super facil demostrarlo) 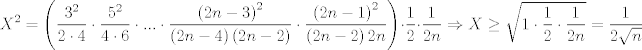
-------------------- La intuición es un arma poderosa en un matemático.-
...Un hermoso cálculo que nació en una noche de inspiración ![TEX: $$\frac{\sqrt[5]{5}}{\sqrt[3]{3}}\cdot \frac{\sqrt[9]{9}}{\sqrt[7]{7}}\cdot \frac{\sqrt[13]{13}}{\sqrt[11]{11}}\cdot \frac{\sqrt[17]{17}}{\sqrt[15]{15}}\cdot \frac{\sqrt[21]{21}}{\sqrt[19]{19}}\cdot \frac{\sqrt[25]{25}}{\sqrt[23]{23}}\cdot ...=\exp \left( -\frac{\pi \gamma }{4}-\frac{\pi }{2}\log 2-\frac{3\pi }{4}\log \pi +\pi \log \Gamma \left( \frac{1}{4} \right) \right)$$](/tex-image/d59471a94884c2506dd649e5016366b1.png) |
|
|
|
 Dec 26 2017, 12:44 PM Dec 26 2017, 12:44 PM
Publicado:
#16
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 110 Registrado: 8-February 16 Miembro Nº: 143.585 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
|
|
|
|
 Aug 22 2021, 11:03 PM Aug 22 2021, 11:03 PM
Publicado:
#17
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.566 Registrado: 20-June 11 Desde: Region del Maule Miembro Nº: 90.738 Sexo:  |
Borrar
Mensaje modificado por Legition Rompediskoteqa el Aug 22 2021, 11:21 PM -------------------- Actualmente en Ingenieria Industrial y en 3er año Ingeniería Civil Mecánica.
From my personal life: I highly recommend this video Click Here! Es altamente deseable tener aptitud para la quimica(termodinámica), la programación, alta comprensión de un problema y planteamiento del mismo, y tener resiliencia al estudiar Ingenieria Civil Industrial. Civil Industrial es en gran parte saber levantar(modelar problemas) procesos logísticos. Puedo dar fe que la Universidad Nacional Andres Bello está adelante de varias U'es Regionales(Calidad similar a la UTAL). Realidad universidades del mundo (18:30): Youtube Quiten Filosofia, Musica y Religión del Curriculum de la Media!! No es recomendado trabajar/colaborar entre matemáticos en general. En general, y a menos que Chile gaste mínimo 2% PIB en I+D, quedarse a investigar en el país, es matarse académicamente. Como recomendación Brasil es un pais muy adelantado en investigación versus AL. Gasto 2023: 0,34%.  |
|
|
|
 Aug 30 2021, 06:26 AM Aug 30 2021, 06:26 AM
Publicado:
#18
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 524 Registrado: 2-October 13 Miembro Nº: 122.939 Nacionalidad:  Sexo:  |
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 04:23 PM |