|
|
|
|
|
|
|
  |
 Jul 14 2016, 10:07 PM Jul 14 2016, 10:07 PM
Publicado:
#1
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
57ª OLIMPIADA INTERNACIONAL DE MATEMÁTICA Hong Kong Primera Prueba: Lunes 11 de julio de 2016 Problema 1: El triángulo 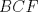 es rectángulo en es rectángulo en 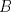 . Sea . Sea 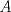 el punto de la recta el punto de la recta 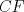 tal que tal que 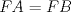 y y 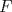 está entre está entre 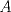 y y 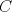 . Se elige el punto . Se elige el punto 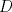 de modo que de modo que 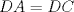 y y 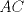 es bisectriz del ángulo es bisectriz del ángulo 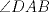 . Se elige el punto . Se elige el punto 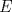 de modo que de modo que 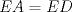 y y 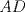 es bisectriz del ángulo es bisectriz del ángulo 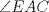 . Sea . Sea 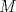 el punto medio de el punto medio de 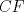 . Sea . Sea 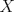 el punto tal que el punto tal que 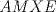 es un paralelogramo (con es un paralelogramo (con 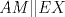 y y 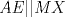 ). Demostrar que las rectas ). Demostrar que las rectas 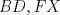 y y 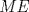 son concurrentes. son concurrentes. Problema 2: Hallar todos los enteros positivos  para los que en cada casilla de un tablero para los que en cada casilla de un tablero 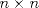 se puede escribir una de las letras se puede escribir una de las letras 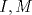 y y 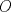 de manera que: de manera que:
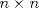 se numeran desde 1 hasta se numeran desde 1 hasta  , en su orden natural. Así, cada casilla corresponde a un par de enteros positivos , en su orden natural. Así, cada casilla corresponde a un par de enteros positivos 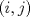 con con 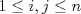 . Para . Para 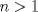 , el tablero tiene , el tablero tiene 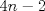 líneas diagonales de dos tipos. Una línea diagonal del primer tipo se compone de todas las casillas líneas diagonales de dos tipos. Una línea diagonal del primer tipo se compone de todas las casillas 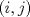 para las que para las que 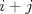 es una constante, mientras que una línea diagonal del segundo tipo se compone de todas las casillas es una constante, mientras que una línea diagonal del segundo tipo se compone de todas las casillas 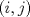 para las que para las que  es una constante. es una constante. Problema 3: Sea 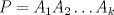 un polígono convexo en el plano. Los vértices un polígono convexo en el plano. Los vértices 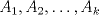 tienen coordenadas enteras y se encuentran sobre una circunferencia. Sea tienen coordenadas enteras y se encuentran sobre una circunferencia. Sea 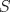 el área de el área de 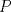 . Sea . Sea  un entero positivo impar tal que los cuadrados de las longitudes de los lados de un entero positivo impar tal que los cuadrados de las longitudes de los lados de 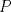 son todos números enteros divisibles por son todos números enteros divisibles por  . Demostrar que . Demostrar que 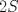 es un entero divisible por es un entero divisible por  . . Segunda Prueba: Martes 12 de julio de 2016 Problema 4: Un conjunto de números enteros positivos se llama fragante si contiene al menos dos elementos, y cada uno de sus elementos tiene algún factor primo en común con al menos uno de los elementos restantes. Sea 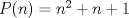 . Determinar el menor número entero positivo . Determinar el menor número entero positivo  para el cual existe algún número entero no negativo para el cual existe algún número entero no negativo  tal que el conjunto tal que el conjunto 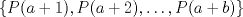 es fragante. Problema 5: En la pizarra está escrita la ecuación 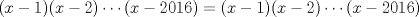 que tiene 2016 factores lineales en cada lado. Determinar el menor valor posible de 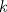 para el cual pueden borrarse exactamente para el cual pueden borrarse exactamente 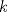 de estos 4032 factores lineales, de modo que al menos quede un factor en cada lado y la ecuación que resulte no tenga soluciones reales. de estos 4032 factores lineales, de modo que al menos quede un factor en cada lado y la ecuación que resulte no tenga soluciones reales.Problema 6: Se tienen 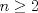 segmentos en el plano tales que cada par de segmentos se intersecan en un punto interior a ambos, y no hay tres segmentos que tengan un punto en común. Mafalda debe elegir uno de los extremos de cada segmento y colocar sobre él una rana mirando hacia el otro extremo. Luego silbará segmentos en el plano tales que cada par de segmentos se intersecan en un punto interior a ambos, y no hay tres segmentos que tengan un punto en común. Mafalda debe elegir uno de los extremos de cada segmento y colocar sobre él una rana mirando hacia el otro extremo. Luego silbará 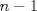 veces. En cada silbido, cada rana saltará inmediatamente hacia adelante hasta el siguiente punto de intersección sobre su segmento. Las ranas nunca cambian las direcciones de sus saltos. Mafalda quiere colocar las ranas de tal forma que nunca dos de ellas ocupen al mismo tiempo el mismo punto de intersección. veces. En cada silbido, cada rana saltará inmediatamente hacia adelante hasta el siguiente punto de intersección sobre su segmento. Las ranas nunca cambian las direcciones de sus saltos. Mafalda quiere colocar las ranas de tal forma que nunca dos de ellas ocupen al mismo tiempo el mismo punto de intersección.(a) Demostrar que si  es impar, Mafalda siempre puede lograr su objetivo. es impar, Mafalda siempre puede lograr su objetivo.(b) Denostrar que si  es par, Mafalda nunca logrará su objetivo. es par, Mafalda nunca logrará su objetivo.
-------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 08:56 PM |






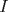 , un tercio tiene
, un tercio tiene 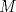 y un tercio tiene
y un tercio tiene 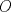 ; y
; y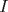 , un tercio tiene
, un tercio tiene 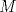 y un tercio tiene
y un tercio tiene 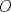 .
.

