|
|
|
|
|
|
|
  |
 Mar 8 2016, 02:08 PM Mar 8 2016, 02:08 PM
Publicado:
#1
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 5 Registrado: 5-March 16 Miembro Nº: 143.877 |
me podrían explicar como puedo determinar su valor de verdad
Mensaje modificado por tonyy el Mar 8 2016, 02:17 PM
Archivo(s) Adjunto(s)
 10261651_976128125815119_1589628855_n.jpg ( 13.55k )
Número de descargas: 13
10261651_976128125815119_1589628855_n.jpg ( 13.55k )
Número de descargas: 13 10261651_976128125815119_1589628855_n.jpg ( 13.55k )
Número de descargas: 3
10261651_976128125815119_1589628855_n.jpg ( 13.55k )
Número de descargas: 3 |
|
|
|
 Mar 9 2016, 06:33 PM Mar 9 2016, 06:33 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 4.874 Registrado: 19-January 07 Desde: Mathematics!! Miembro Nº: 3.830 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Fácil, justo estoy haciendo un ejercicio parecido, pero de medida XD.
Fíjate que te dicen que es para todo 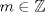 , entonces tomemos cualquier entero, digamos , entonces tomemos cualquier entero, digamos 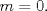 Luego, debería de ser capaz de encontrar al menos un natural para que la propiedad se cumpla. Claramente esto es falso, porque si tomas Luego, debería de ser capaz de encontrar al menos un natural para que la propiedad se cumpla. Claramente esto es falso, porque si tomas 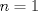 resulta que resulta que 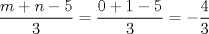 , lo que en efecto, no es un número natural. Así, el valor de verdad de la proposición es F=Falso. , lo que en efecto, no es un número natural. Así, el valor de verdad de la proposición es F=Falso.Observación: Fíjate además que da lo mismo cuál entero tomas..., la clave es encontrar al menos un natural para el cual la propiedad falla, si lo encuentras, es porque no es siempre cierta la cuantificación de esa propiedad. Esto lo puedes ver como forma de "contraejemplo". Algo más formal seria negar la proposición, entonces te queda: 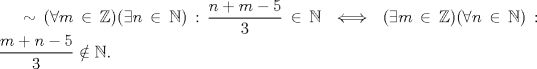 Saludos! Mensaje modificado por Julio_fmat el Mar 9 2016, 07:10 PM --------------------  "... Lo veo, pero no puedo creerlo ... se trata de mostrar que las superficies, los volúmenes e incluso las variedades continuas de n dimensiones pueden ponerse en correspondencia unívoca con curvas continuas, o sea, con variedades de una sola dimensión, y que por consiguiente, las superficies, los volúmenes y las variedades de n dimensiones tienen también la misma potencia que las curvas ..." G. Cantor. Las Matemáticas son el lenguaje de la naturaleza, todo lo que nos rodea se puede representar y entender mediante números. Si se hace un gráfico con los números de un sistema, se forman modelos; éstos modelos están por todas partes en la naturaleza. Max Cohen.  Licenciado en Matemática (2021). Universidad de Concepción, Chile. |
|
|
|
 Mar 9 2016, 08:17 PM Mar 9 2016, 08:17 PM
Publicado:
#3
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 409 Registrado: 18-January 11 Desde: soy del colegio san viator de macul no de ovalle. Miembro Nº: 83.168 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Fácil, justo estoy haciendo un ejercicio parecido, pero de medida XD. Fíjate que te dicen que es para todo 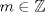 , entonces tomemos cualquier entero, digamos , entonces tomemos cualquier entero, digamos 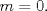 Luego, debería de ser capaz de encontrar al menos un natural para que la propiedad se cumpla. Claramente esto es falso, porque si tomas Luego, debería de ser capaz de encontrar al menos un natural para que la propiedad se cumpla. Claramente esto es falso, porque si tomas 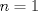 resulta que resulta que 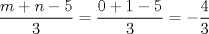 , lo que en efecto, no es un número natural. Así, el valor de verdad de la proposición es F=Falso. , lo que en efecto, no es un número natural. Así, el valor de verdad de la proposición es F=Falso.Observación: Fíjate además que da lo mismo cuál entero tomas..., la clave es encontrar al menos un natural para el cual la propiedad falla, si lo encuentras, es porque no es siempre cierta la cuantificación de esa propiedad. Esto lo puedes ver como forma de "contraejemplo". Algo más formal seria negar la proposición, entonces te queda: 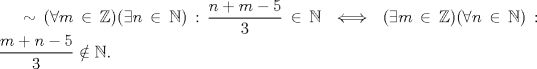 Saludos! la proposicion es verdadera. si 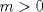 , tomamos , tomamos 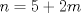 y si y si 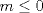 , tomamos , tomamos 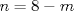 . .
--------------------    Tercer lugar Olimpiadas del Conocimiento Usach 2011 - Matemáticas |
|
|
|
 Mar 9 2016, 08:56 PM Mar 9 2016, 08:56 PM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 524 Registrado: 2-October 13 Miembro Nº: 122.939 Nacionalidad:  Sexo:  |
julio is back
|
|
|
|
 Mar 9 2016, 09:37 PM Mar 9 2016, 09:37 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 4.874 Registrado: 19-January 07 Desde: Mathematics!! Miembro Nº: 3.830 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
la proposicion es verdadera. si 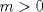 , tomamos , tomamos 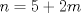 y si y si 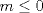 , tomamos , tomamos 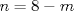 . .Ya OK, reconozco que no lo pensé bien. Cualquiera puede equivocarse en algún momento, pero tampoco pienso que estaría malo verlo como lo estaba pensando, solo que fallé en la generalización; comprobando con un caso particular solamente. julio is back No faltan los estúpidos XD. --------------------  "... Lo veo, pero no puedo creerlo ... se trata de mostrar que las superficies, los volúmenes e incluso las variedades continuas de n dimensiones pueden ponerse en correspondencia unívoca con curvas continuas, o sea, con variedades de una sola dimensión, y que por consiguiente, las superficies, los volúmenes y las variedades de n dimensiones tienen también la misma potencia que las curvas ..." G. Cantor. Las Matemáticas son el lenguaje de la naturaleza, todo lo que nos rodea se puede representar y entender mediante números. Si se hace un gráfico con los números de un sistema, se forman modelos; éstos modelos están por todas partes en la naturaleza. Max Cohen.  Licenciado en Matemática (2021). Universidad de Concepción, Chile. |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 08:57 PM |