Identificarse Registrarse

Psu
Enseñanza Básica
Enseñanza Media
Universidad
Olimpiadas
Comunidad



 
 Reply to this topicStart new topic
> Suma
juancodmw
mensaje Jan 13 2016, 10:41 AM
Publicado: #1


Dios Matemático Supremo
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 783
Registrado: 23-April 13
Desde: Constitución
Miembro Nº: 118.027
Nacionalidad:
Universidad: Universidad de Chile-FCFM
Sexo:



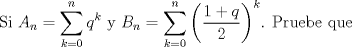TEX: Si $\displaystyle A_n =\sum_{k=0}^{n}q^k$ y $\displaystyle B_n=\sum_{k=0}^{n}\left(\dfrac{1+q}{2}\right)^k$. Pruebe que

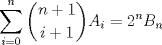TEX: $\displaystyle \sum_{i=0}^{n}\binom{n+1}{i+1}A_i =2^n B_n$


--------------------
Go to the top of the page
 
+Quote Post
Ignacio Acevedo
mensaje Jan 13 2016, 07:45 PM
Publicado: #2


Principiante Matemático Destacado
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 16
Registrado: 14-March 15
Desde: Cerrillos
Miembro Nº: 136.101
Nacionalidad:
Universidad: Universidad de Chile-FCFM
Sexo:



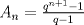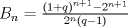Primero se tiene que TEX: $ A_{n}=\frac{q^{n+1}-1}{q-1} $ y TEX: $ B_{n}=\frac{\left ( 1+q \right )^{n+1}-2^{n+1}}{2^{n}\left ( q-1 \right )} $

Ahora se tiene: 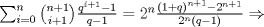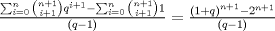TEX: $ \sum_{i=0}^{n}\binom{n+1}{i+1}\frac{q^{i+1}-1}{q-1} =2^{n} \frac{\left( 1+q \right )^{n+1}-2^{n+1}}{2^{n}\left ( q-1 \right )} \Rightarrow $ TEX: $ \frac{\sum_{i=0}^{n}\binom{n+1}{i+1}q^{i+1}-\sum_{i=0}^{n}\binom{n+1}{i+1}1}{(q-1)}=\frac{\left( 1+q \right )^{n+1}-2^{n+1}}{\left ( q-1 \right )} $ y esto expresa al binomio de newton, comprobando lo pedido
Go to the top of the page
 
+Quote Post
 

Reply to this topicStart new topic
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):

 

Versión Lo-Fi Fecha y Hora actual: 23rd November 2024 - 03:31 PM
Powered By IP.Board 2.2.1 © 2007  IPS, Inc.