|
|
|
|
|
|
|
  |
 Aug 26 2015, 12:16 PM Aug 26 2015, 12:16 PM
Publicado:
#1
|
|
 Doctor en Matemáticas Grupo: Colaborador Silver Mensajes: 193 Registrado: 17-August 12 Desde: Loncuma :3 Miembro Nº: 110.077 Nacionalidad:  Sexo:  |
Una recta corta a los lados
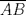 y y 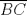 , y a la prolongacion de , y a la prolongacion de 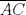 del triangulo del triangulo 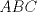 en los puntos en los puntos 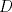 , , 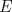 y y 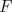 . Pruebe que los puntos medios de . Pruebe que los puntos medios de 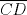 , , 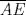 y y 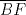 son colineales. son colineales.
|
|
|
|
 Aug 26 2015, 08:02 PM Aug 26 2015, 08:02 PM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
  Sin_t_tulo.png ( 16.85k )
Número de descargas: 1
Sin_t_tulo.png ( 16.85k )
Número de descargas: 1 Agradecimientos a niklaaaaaashhhhhhh Mensaje modificado por Kaissa el Aug 28 2015, 12:17 PM -------------------- |
|
|
|
 Aug 27 2015, 12:03 PM Aug 27 2015, 12:03 PM
Publicado:
#3
|
|
 Doctor en Matemáticas Grupo: Colaborador Silver Mensajes: 193 Registrado: 17-August 12 Desde: Loncuma :3 Miembro Nº: 110.077 Nacionalidad:  Sexo:  |
Creo que, XYOM no es paralelogramo (tambien se ve en el dibujito), MX=DB/2 y OY=BC/2 (creo que lo viste como DB/2), o bien estoy viendo mal la configuracion |
|
|
|
 Aug 28 2015, 12:12 PM Aug 28 2015, 12:12 PM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Me disculpo.
Fé de erratas: cámbiese en todo el texto "paralelógramo" por "trapecio" Gracias. PD: Si a alguien le cabe alguna duda acerca del uso de Papus con paralelas piense en el teorema con una recta al infinito. Mensaje modificado por Kaissa el Aug 28 2015, 12:47 PM -------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 6th March 2025 - 09:09 PM |