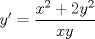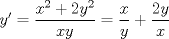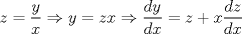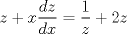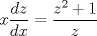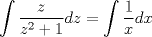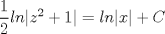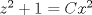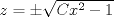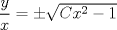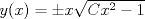I3 cálculo II licenciatura

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Cálculo II

I3 cálculo II licenciatura

Opciones

nacharon Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 5 2015, 06:25 PM Publicado: #1
Dios Matemático Grupo: Usuario FMAT Mensajes: 321 Registrado: 25-February 13 Miembro Nº: 115.593 Nacionalidad: Universidad: Sexo:	La i3 que tuvimos ayer, pa q se animen y hagan alguno. El p3 esta bien choro $TEX: <br />\noindent 1. Hallar la soluci\'on general de la ecuaci\'on diferencial $\displaystyle y'=\frac{x^2+2y^2}{xy}$.\\<br />\\<br />2. Hallar la soluci\'on general de la ecuaci\'on diferencial $\displaystyle y''-y=\frac{2}{1+e^x}$ en $\mathbb R$.\\<br />\\<br />3. Sea $f_n:X\to\mathbb R$ una sucesi\'on de funciones tales que $f_1\ge f_2\ge f_3\ge\ldots$ y $f_n\to 0$ uniformemente en $X$. Pruebe que la serie $\sum_{n=1}^\infty(-1)^nf_n$ converge uniformemente en $X$.\\<br />\\<br />4. Sea $p(x)$ un polinomio de grado $d\ge 2$. Considere la sucesi\'on de funciones $f:\mathbb R\to\mathbb R$ dada por $f_n(x)=p(x+1/n)$. Demuestre que $f_n\to p$ puntualmente pero no uniformemente.<br />$

Ditoow Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 5 2015, 07:53 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 579 Registrado: 17-April 11 Miembro Nº: 87.233 Colegio/Liceo: Universidad: Sexo:	P1. Veamos que tal, justo estaba estudiando sobre esto jaja :3 Hallar la solución general de la ecuación diferencial $TEX: $y'=\dfrac{x^2+2y^2}{xy}$$ $TEX: $y'=\dfrac{x^2+2y^2}{xy}=\dfrac{x}{y}+\dfrac{2y}{x}$$ Sea $TEX: $z=\dfrac{y}{x}\Rightarrow y=zx \Rightarrow \dfrac{dy}{dx}=z+x\dfrac{dz}{dx}$$ Reemplazando tenemos: $TEX: $z+x\dfrac{dz}{dx}=\dfrac{1}{z}+2z$$ $TEX: $x\dfrac{dz}{dx}=\dfrac{z^2+1}{z}$$ $TEX: $\displaystyle \int \dfrac{z}{z^2+1}dz=\displaystyle \int \dfrac{1}{x}dx$$ $TEX: $\dfrac{1}{2}ln\|z^2+1\|=ln\|x\|+C$$ $TEX: $ln(z^2+1)=ln(x^2)+C$$ $TEX: $z^2+1=Cx^2$$ $TEX: $z=\pm \sqrt{Cx^2-1}$$ $TEX: $\dfrac{y}{x}=\pm \sqrt{Cx^2-1}$$ Finalmente $TEX: $y(x)=\pm x\sqrt{Cx^2-1}$$

Lichiel Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 5 2015, 09:10 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 736 Registrado: 3-December 12 Miembro Nº: 113.971 Nacionalidad: Universidad: Sexo:	P4 $TEX: \noindent Sea $x_0 \in \mathbb{R}$. Notemos que los polinomios son continuos <br />$$ \lim_{n \rightarrow \infty} f_n(x) = \lim_{n \rightarrow \infty} P(x_0+\frac{1}{n})=P(\lim_{n \rightarrow \infty} x_0+\frac{1}{n})=P(x)$$ Por lo tanto $f_n$ converge puntualmente a $P$ en $\mathbb{R}$ <br />Tomemos la diferencia <br />$$\|f_n(x)-P(x)\|=\|P(x+\frac{1}{n})-P(x)\|=\|Q(x)\|$$ donde $Q$ es un polinomio de grado $d-1$ pero los polinomios no son acotados en $\mathbb{R}$. Entonces para todo $M>0$ existe un $N \in \mathbb{N}$ tal que \begin{equation} M \leq \|f_n(x)-P(x)\| <br />\tag{$\forall n > N \forall x \in \mathbb{R}$} \end{equation}<br />Por lo tanto $f_n$ no converge uniformemente a $P$ en $\mathbb{R}$$ Mensaje modificado por Lichiel el Jun 5 2015, 09:10 PM -------------------- 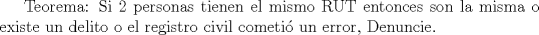$TEX: \begin{center} $ \aleph_0$ $<$ $\|?\|$ $< \aleph_1 $ \end{center}$ $TEX: Teorema: Si 2 personas tienen el mismo RUT entonces son la misma o existe un delito o el registro civil cometió un error, Denuncie.$ Quiero plata

Lichiel Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 5 2015, 09:26 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 736 Registrado: 3-December 12 Miembro Nº: 113.971 Nacionalidad: Universidad: Sexo:	Problema 2 $TEX: \noindent Emplearemos el método de variaciones Resolvemos la ecuación homogénea $y''-y=0$ la cual tiene como solución $y_1=span (e^x,e^{-x}) $ Por lo tanto $W(x)=-2$. Donde $W(x)$ es el Wronskiano, entonces la solución general debe ser de la forma $y=c_1e^xt_1(x)+c_2e^{-x}t_1(x)$ con $c_1,c_2$ constantes y $$t_1(x)=\int \frac{e^{-x}}{1+e^x} dx=\ln\|e^{-x}+1\|-e^{-x} $$ $$t_2(x)=-\int \frac{e^x}{1+e^x} dx =\ln \| e^x+1\|$$$ Mensaje modificado por Lichiel el Jun 5 2015, 09:27 PM -------------------- 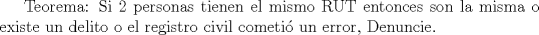$TEX: \begin{center} $ \aleph_0$ $<$ $\|?\|$ $< \aleph_1 $ \end{center}$ $TEX: Teorema: Si 2 personas tienen el mismo RUT entonces son la misma o existe un delito o el registro civil cometió un error, Denuncie.$ Quiero plata

nacharon Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 7 2015, 04:45 PM Publicado: #5
Dios Matemático Grupo: Usuario FMAT Mensajes: 321 Registrado: 25-February 13 Miembro Nº: 115.593 Nacionalidad: Universidad: Sexo:	esto hice yo en la 3 (espero que esté bien xd) $TEX: <br />Sea $S_n:=\sum_{k=1}^n(-1)^kf_k$. Como $-f_{2k-1}+f_{2k}\le 0$, se tiene que la subsucesi\'on $\{S_{2n}\}$ es decreciente. De manera an\'aloga se puede comprobar que la subsucesi\'on $\{S_{2n-1}\}$ es creciente (omitiendo el detalle de decir $\forall x\in X$ todo el rato).\\<br />\\<br />Afirmaci\'on: dado $n_0\in\mathbb N$, para todo $n\ge 2n_0$ se tiene $S_n\in [S_{2n_0-1},S_{2n_0}]$. Para probar alguna de estas desigualdades, por ejemplo la primera, podemos decir primero que para todo $n$ impar mayor que $2n_0-1$ se cumple $S_{2n_0-1}\le S_{n}$ (es claro por el crecimiento de $\{S_{2n-1}\}$). Para ver qu\'e pasa con $S_n$ cuando $n$ es par mayor que $2n_0$, notemos que $S_n\ge S_{n-1}$ por el hecho de que el \'ultimo t\'ermino de $S_n$ es positivo, de modo que $S_n\ge S_{n-1}\ge S_{2n_0-1}$. Esto dice que $S_n\ge S_{2n_0-1}$ para todo $n$ natural mayor que $2n_0$. La segunda desigualdad se prueba de forma an\'aloga.\\<br />\\<br />Como $f_n\to 0$ uniformemente, dado $\varepsilon>0$ existe $n_0$ tal que $\|f_{2n_0}\|<\varepsilon$, luego para este $n_0$<br />$$\|S_{2n_0}-S_{2n_0-1}\|=\|f_{2n_0}\|<\varepsilon.$$<br />Esto y la afirmaci\'on de arriba implican que si $m,n$ son naturales mayores que $2n_0$ entonces $\|S_m-S_n\|\le \|S_{2n_0}-S_{2n_0-1}\|<\varepsilon,$<br />por lo tanto $\{S_n\}$ es de Cauchy, lo que equivale a decir que converge uniformemente.<br />$ Puede ser interesante fijarse en que X no necesariamente es un subconjunto de R. Aparte, el resultado ya me parece bkn como generalización del criterio de Leibniz para series numéricas. Mensaje modificado por nacharon el Jun 7 2015, 04:46 PM

« Posterior · Cálculo II · Anterior »

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 05:42 PM