|
|
|
|
|
|
|
  |
 May 18 2015, 12:07 PM May 18 2015, 12:07 PM
Publicado:
#1
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 141 Registrado: 9-December 12 Miembro Nº: 114.238 Colegio/Liceo:  Universidad:  Sexo:  |
Control 2 MA 2601, 2015/1 Prof. Salomé Martínez Aux. Álvaro Bustos, Cristóbal Rojas y Nicolás Torres Duración 3 hrs. P1. a) Determine la solución general de las siguientes ecuaciones: 1) (1 pt) 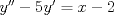 2) (1 pt) 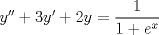 b) (2 pt) Determine bajo qué condiciones para el parámetro 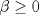 el problema el problema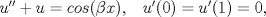 tiene solución. c) Considere el operador diferencial 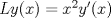 . .1) (0,5 pt) Determine la solución de 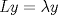 con con 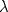 un número real. un número real.2) (0,5 pt) Considere la ecuación 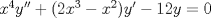 Demuestre que esta ecuación puede ser escrita como 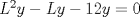 , donde , donde 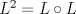 . .3) (1 pt) Encuentre una base de soluciones de esta ecuación en 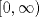 . Ind.: Pruebe que si . Ind.: Pruebe que si 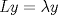 , entonces , entonces 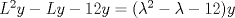 . .P2 Sea 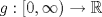 continua. Considere la ecuación lineal de segundo orden: continua. Considere la ecuación lineal de segundo orden: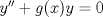 en en 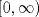 , (1) , (1)y sean 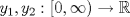 dos soluciones linealmente independientes de (1). dos soluciones linealmente independientes de (1).a) (0,5 pt) Demuestre que el wronskiano 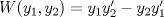 es constante. es constante.b) (1 pt) Si definimos 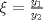 , definida en los intervalos donde , definida en los intervalos donde 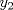 no se anula, entonces no se anula, entonces 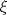 satisface la ecuación: satisface la ecuación: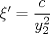 con  una constante. una constante.c) Suponga que cualquier solución de (1) tiene un número finito de ceros en 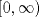 . Probaremos que se puede elegir . Probaremos que se puede elegir 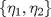 una base de soluciones de (1) con las siguiente propiedades: una base de soluciones de (1) con las siguiente propiedades:(i) 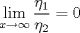 (ii) 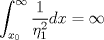 y y 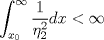 , donde , donde 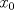 es un punto elegido para que es un punto elegido para que 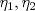 no se anulen en no se anulen en 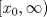 . .(iii) 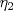 es no acotada en es no acotada en 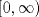 . .Probaremos cada una de estas propiedades en las partes que vienen a continuación. 1) (1 pt) Para probar (i) demuestre que si 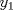 e e 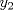 son una base de soluciones , entonces sin pérdida de generalidad podemos suponer que son una base de soluciones , entonces sin pérdida de generalidad podemos suponer que 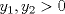 para para 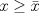 con con 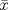 elegido para que elegido para que 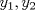 no se anulen en no se anulen en 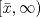 . Luego, usando la parte b), demuestre que se tiene una de las siguientes posibilidades: . Luego, usando la parte b), demuestre que se tiene una de las siguientes posibilidades:a) 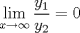 ; b) ; b) 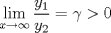 ; c) ; c) 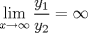 . .Para concluir (i) demuestre que si se tiene el caso a) basta tomar 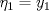 , , 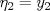 ; si se tiene el caso b) se define ; si se tiene el caso b) se define 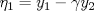 , , 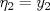 ; y en el caso c) basta considerar ; y en el caso c) basta considerar 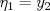 y y 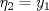 . Explique en cada caso porque las funciones . Explique en cada caso porque las funciones 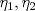 son l.i. son l.i.2) (1pt) Para demostrar (ii) use la parte b) para expresar las integrales, considerando las funciones 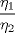 y y 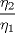 . Use la parte (i). . Use la parte (i).3) (1 pt) Para concluir (iii), puede probar que si 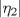 es acotada, entonces es acotada, entonces 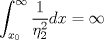 lo que contradice (ii). lo que contradice (ii).d) (1,5 pt) Dé un ejemplo de una función 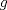 para la cual de satisface que todas las soluciones de (1) tienen un número finito de ceros en para la cual de satisface que todas las soluciones de (1) tienen un número finito de ceros en 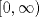 . Para su ejemplo, encuentre soluciones l.i. . Para su ejemplo, encuentre soluciones l.i. 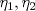 que satisfagan (i), (ii) y (iii). que satisfagan (i), (ii) y (iii).Mensaje modificado por Felele el May 18 2015, 12:12 PM |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 11:40 PM |








