Sobre inferencia estadistica, empresa de autos

Sobre inferencia estadistica, empresa de autos

Opciones

eraldcoil Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 28 2015, 09:08 PM Publicado: #1
Dios Matemático Grupo: Usuario FMAT Mensajes: 476 Registrado: 15-November 10 Miembro Nº: 80.334 Nacionalidad: Universidad: Sexo:	estadistica.jpg ( 547.84k ) Número de descargas: 11 Cabros, como hago la pruimera pregunta? no logro caxar como hacerlo, es media rara la tabla, Me basta con que alguien sake el promedio de venta para la primera sucursal, yo hago las demas Desde ya graciassss

Julio_fmat Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 30 2015, 06:16 PM Publicado: #2
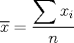Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 4.874 Registrado: 19-January 07 Desde: Mathematics!! Miembro Nº: 3.830 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Olvida lo otro que puse... Pero si preguntan por promedio se debería usar que $TEX: $\overline{x}=\dfrac{\displaystyle\sum x_i}{n}$$ o no? Mensaje modificado por Julio_fmat el Mar 30 2015, 06:22 PM -------------------- "... Lo veo, pero no puedo creerlo ... se trata de mostrar que las superficies, los volúmenes e incluso las variedades continuas de n dimensiones pueden ponerse en correspondencia unívoca con curvas continuas, o sea, con variedades de una sola dimensión, y que por consiguiente, las superficies, los volúmenes y las variedades de n dimensiones tienen también la misma potencia que las curvas ..." G. Cantor. Las Matemáticas son el lenguaje de la naturaleza, todo lo que nos rodea se puede representar y entender mediante números. Si se hace un gráfico con los números de un sistema, se forman modelos; éstos modelos están por todas partes en la naturaleza. Max Cohen. $TEX: $$\Phi=\displaystyle \int \limits_{-\infty}^x \dfrac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}t^2}dt=\lim_{n\to +\infty}P\left(\dfrac{\displaystyle \sum_{i=1}^n x_i-n\mu}{n\sigma}\le x\right).$$$ Licenciado en Matemática (2021). Universidad de Concepción, Chile.

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 23rd November 2024 - 05:47 PM