|
|
|
|
|
|
|
  |
 Feb 17 2015, 09:22 AM Feb 17 2015, 09:22 AM
Publicado:
#1
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 61 Registrado: 10-May 14 Miembro Nº: 129.363 Nacionalidad:  Universidad:  Sexo:  |
¿Es posible encontrar una función
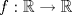 cuyo grafo tenga exactamente cuyo grafo tenga exactamente  ejes de simetría?. ejes de simetría?. |
|
|
|
 Feb 21 2015, 08:08 PM Feb 21 2015, 08:08 PM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Una rosa de tres pétalos tal que el eje de simetría de cada pétalo esté a 120° de los otros dos.
Edito... uhm... tú quieres una cuestión que sea FUN-CIÓN... Pruebe que no existen ni siquiera con dos ejes. HINT: línea vertical. Mensaje modificado por Kaissa el Feb 21 2015, 08:10 PM -------------------- |
|
|
|
 Mar 3 2015, 09:51 AM Mar 3 2015, 09:51 AM
Publicado:
#3
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 61 Registrado: 10-May 14 Miembro Nº: 129.363 Nacionalidad:  Universidad:  Sexo:  |
Una rosa de tres pétalos tal que el eje de simetría de cada pétalo esté a 120° de los otros dos. Edito... uhm... tú quieres una cuestión que sea FUN-CIÓN... Pruebe que no existen ni siquiera con dos ejes. HINT: línea vertical. La impresión que tienes al principio de la respuesta está un poco más cerca de lo esperado, salvo lo que detallas después. Si bien puede parecer obvio, como indicación podrías tratar de dibujar el grafo en el plano complejo tal que 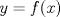 corresponde al punto corresponde al punto 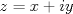 . También podrías jugar con la imagen de . También podrías jugar con la imagen de 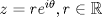 bajo el grupo de reflexiones generado por bajo el grupo de reflexiones generado por  ejes que convenientemente puedes definir a partir de la definición de ejes que convenientemente puedes definir a partir de la definición de  . La gracia es que te van a dar a lo más . La gracia es que te van a dar a lo más  segmentos, con lo cual podrías probar que no tiene más de segmentos, con lo cual podrías probar que no tiene más de  ejes de simetría. ejes de simetría.
Mensaje modificado por black cat el Mar 3 2015, 10:02 AM |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 04:51 PM |











