Polinomio II - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Ejercitación > Álgebra > Polinomios

Reply to this topic

Start new topic

Polinomio II, propuesto

Adrianocor Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 11 2015, 04:10 PM Publicado: #1
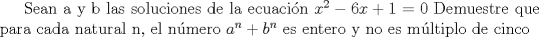
Dios Matemático Grupo: Usuario FMAT Mensajes: 325 Registrado: 18-March 14 Miembro Nº: 127.725 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: Sean a y b las soluciones de la ecuación $x^{2}-6x+1=0$ Demuestre que para cada natural n, el número $a^{n}+b^{n}$ es entero y no es múltiplo de cinco$

vocin Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 11 2015, 04:55 PM Publicado: #2
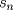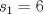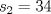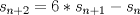Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 648 Registrado: 26-October 13 Desde: Tokyo-3 Miembro Nº: 123.749 Nacionalidad: Sexo:	Consideremos la sucesión $TEX: \( s_n \)$ definida como sigue: - $TEX: \( s_1=6 \)$ - $TEX: \( s_2=34 \)$ -Para todo $TEX: \( n \)$ natural, $TEX: \( s_{n+2}=6s_{n+1}-s_{n} \)$ Demostremos algunas cosas entretenidas de dicha sucesión: a) Para todo 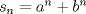$TEX: \( n \)$ natural, tenemos que $TEX: \( s_n=a^n+b^n \)$ Utilizaremos inducción. 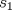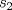Los casos bases $TEX: \( s_1 \)$ y $TEX: \( s_2 \)$ , se los dejamos al lector. 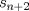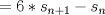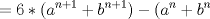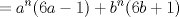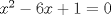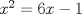Para el paso inductivo, basta utilizar la regla de la sucesión: $TEX: \( \displaystyle s_{n+2} \)$ $TEX: \( \displaystyle = 6s_{n+1}-s_n \)$ $TEX: \( \displaystyle = 6(a^{n+1}+b^{n+1})-(a^n+b^n \)$ $TEX: \( \displaystyle = a^n(6a-1)+b^n (6b+1) \)$ Pero $TEX: \( a \)$ y $TEX: \( b \)$ son raíces del polinomio $TEX: \( x^2-6x+1=0 \)$ , de donde $TEX: \( x^2=6x-1 \)$ es válida para ambas raíces; esto nos permite sustituir las expresiones del lado derecho por las del lado izquierdo. 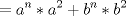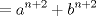$TEX: \( \displaystyle = a^na^2+b^nb^2 \)$ $TEX: \( \displaystyle = a^{n+2}+b^{n+2} \)$ Concluyendo así la demostración del punto a. b) 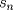$TEX: \( s_n \)$ nunca es múltiplo de 5 Basta ver que los residuos módulo 5 forman un ciclo: 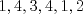$TEX: \( 1, 4, 3, 4, 1, 2 \)$ , que se repite indefinidamente, debido a la regla de formación. 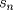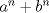Para concluir el problema, basta recordar la relación entre $TEX: \( s_n \)$ y $TEX: \( a^n+b^n \)$ . Ya que la primeros son sólo enteros (por propiedad de clausura) no múltiplos de 5 (probado en "b"); los segundos también lo serán (por lo probado en "a") Mensaje modificado por vocin* el Feb 11 2015, 04:58 PM -------------------- Pro Tip: Es siempre recomendable saltarse los posts de Insanee/Legition I wish, that I could turn back time 'cos now the guilt is all mine can't live without the trust from those you love I know we can't forget the past you can't forget love & pride because of that, it's killing me inside

Adrianocor Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 11 2015, 05:04 PM Publicado: #3
Dios Matemático Grupo: Usuario FMAT Mensajes: 325 Registrado: 18-March 14 Miembro Nº: 127.725 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	correcto , saludos

« Posterior · Polinomios · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Versión Lo-Fi

Fecha y Hora actual: 9th April 2025 - 12:24 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.