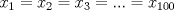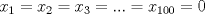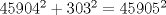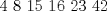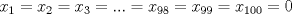|
|
|
|
|
|
|
  |
 Jan 23 2015, 01:09 AM Jan 23 2015, 01:09 AM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 747 Registrado: 1-February 12 Miembro Nº: 100.827 Nacionalidad:  Universidad:  Sexo:  |
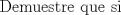 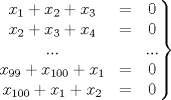 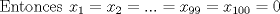
|
|
|
|
 Jan 23 2015, 04:09 PM Jan 23 2015, 04:09 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 783 Registrado: 23-April 13 Desde: Constitución Miembro Nº: 118.027 Nacionalidad:  Universidad:  Sexo:  |
saludos --------------------    |
|
|
|
 Jan 23 2015, 11:53 PM Jan 23 2015, 11:53 PM
Publicado:
#3
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Cabros le eché el ojo a este problema y no me salió. Algunos de ustedes dirán "buuuuuu, ¿pero cómo no le salió al ceniciento? si era más fácil que adivinar de qué color era el caballo blanco de Napoleón!!!". Permítanme contarles qué pasó.
Todo aquel que sepa un poquito de álgebra lineal podrá interpretar matricialmente la situación. Dado 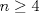 considere la matriz considere la matriz ![TEX: $A_n=[e_{n-1}, e_n, e_1,\ldots, e_{n-2}]+[e_n, e_1, e_2,\ldots, e_{n-1}]+[e_1, e_2, e_3,\ldots, e_{n}]$](/tex-image/e4bed648219b3f3bbe8ecced4ebf525d.png) El problema se reduce a probar que 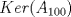 es trivial, lo que es equivalente a probar que es trivial, lo que es equivalente a probar que 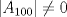 . Me puse a calcular determinantes (ni loco hago eso a mano, ocupé este link)y aquí viene la sorpresa!! Jugando hasta . Me puse a calcular determinantes (ni loco hago eso a mano, ocupé este link)y aquí viene la sorpresa!! Jugando hasta 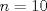 obtuve que obtuve que 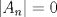 si si 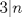 (piense qué pasaría en este caso) y (piense qué pasaría en este caso) y 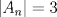 si si 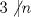 . Es solo una conjetura hecha a la rápida pero es evidente que si mi conjetura es cierta entonces el problema queda listoco. También calculé los polinomios característicos y los valores propios pero desde . Es solo una conjetura hecha a la rápida pero es evidente que si mi conjetura es cierta entonces el problema queda listoco. También calculé los polinomios característicos y los valores propios pero desde 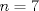 en adelante parece que hay problemas en calcular los valores propios. Es sencillo ver que en adelante parece que hay problemas en calcular los valores propios. Es sencillo ver que 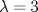 es valor propio (por qué?) pero qué pasa con el resto? es valor propio (por qué?) pero qué pasa con el resto?Eso, si alguien quiere jugar y tratar de comprobar si mi conjetura está bien o mal, bacán. Les estaré agradecidos y podré seguir viendo 9gag con la conciencia tranquila. Paz a todos. Mensaje modificado por Cenizas con Mostaza el Jan 24 2015, 12:18 AM -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Jan 24 2015, 12:05 AM Jan 24 2015, 12:05 AM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 747 Registrado: 1-February 12 Miembro Nº: 100.827 Nacionalidad:  Universidad:  Sexo:  |
Te ayudaria, pero entendi solo el primer y ultimo parrafo xd
Saludos |
|
|
|
 Jan 24 2015, 10:21 AM Jan 24 2015, 10:21 AM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 783 Registrado: 23-April 13 Desde: Constitución Miembro Nº: 118.027 Nacionalidad:  Universidad:  Sexo:  |
media volá del cenizas...
--------------------    |
|
|
|
 Jan 24 2015, 11:03 AM Jan 24 2015, 11:03 AM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 736 Registrado: 3-December 12 Miembro Nº: 113.971 Nacionalidad:  Universidad:  Sexo:  |
Cabros le eché el ojo a este problema y no me salió. Algunos de ustedes dirán "buuuuuu, ¿pero cómo no le salió al ceniciento? si era más fácil que adivinar de qué color era el caballo blanco de Napoleón!!!". Permítanme contarles qué pasó. Todo aquel que sepa un poquito de álgebra lineal podrá interpretar matricialmente la situación. Dado 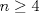 considere la matriz considere la matriz ![TEX: $A_n=[e_{n-1}, e_n, e_1,\ldots, e_{n-2}]+[e_n, e_1, e_2,\ldots, e_{n-1}]+[e_1, e_2, e_3,\ldots, e_{n}]$](/tex-image/e4bed648219b3f3bbe8ecced4ebf525d.png) El problema se reduce a probar que 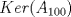 es trivial, lo que es equivalente a probar que es trivial, lo que es equivalente a probar que 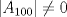 . Me puse a calcular determinantes (ni loco hago eso a mano, ocupé este link)y aquí viene la sorpresa!! Jugando hasta . Me puse a calcular determinantes (ni loco hago eso a mano, ocupé este link)y aquí viene la sorpresa!! Jugando hasta 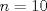 obtuve que obtuve que 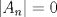 si si 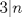 (piense qué pasaría en este caso) y (piense qué pasaría en este caso) y 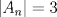 si si 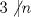 . Es solo una conjetura hecha a la rápida pero es evidente que si mi conjetura es cierta entonces el problema queda listoco. También calculé los polinomios característicos y los valores propios pero desde . Es solo una conjetura hecha a la rápida pero es evidente que si mi conjetura es cierta entonces el problema queda listoco. También calculé los polinomios característicos y los valores propios pero desde 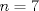 en adelante parece que hay problemas en calcular los valores propios. Es sencillo ver que en adelante parece que hay problemas en calcular los valores propios. Es sencillo ver que 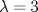 es valor propio (por qué?) pero qué pasa con el resto? es valor propio (por qué?) pero qué pasa con el resto?Eso, si alguien quiere jugar y tratar de comprobar si mi conjetura está bien o mal, bacán. Les estaré agradecidos y podré seguir viendo 9gag con la conciencia tranquila. Paz a todos. Interesante ** voy a jugar con esas matrices. --------------------    Quiero plata |
|
|
|
 Jan 24 2015, 03:40 PM Jan 24 2015, 03:40 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.879 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
Cabros le eché el ojo a este problema y no me salió. Algunos de ustedes dirán "buuuuuu, ¿pero cómo no le salió al ceniciento? si era más fácil que adivinar de qué color era el caballo blanco de Napoleón!!!". Permítanme contarles qué pasó. Todo aquel que sepa un poquito de álgebra lineal podrá interpretar matricialmente la situación. Dado 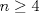 considere la matriz considere la matriz ![TEX: $A_n=[e_{n-1}, e_n, e_1,\ldots, e_{n-2}]+[e_n, e_1, e_2,\ldots, e_{n-1}]+[e_1, e_2, e_3,\ldots, e_{n}]$](/tex-image/e4bed648219b3f3bbe8ecced4ebf525d.png) El problema se reduce a probar que 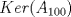 es trivial, lo que es equivalente a probar que es trivial, lo que es equivalente a probar que 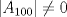 . Me puse a calcular determinantes (ni loco hago eso a mano, ocupé este link)y aquí viene la sorpresa!! Jugando hasta . Me puse a calcular determinantes (ni loco hago eso a mano, ocupé este link)y aquí viene la sorpresa!! Jugando hasta 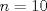 obtuve que obtuve que 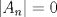 si si 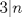 (piense qué pasaría en este caso) y (piense qué pasaría en este caso) y 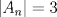 si si 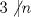 . Es solo una conjetura hecha a la rápida pero es evidente que si mi conjetura es cierta entonces el problema queda listoco. También calculé los polinomios característicos y los valores propios pero desde . Es solo una conjetura hecha a la rápida pero es evidente que si mi conjetura es cierta entonces el problema queda listoco. También calculé los polinomios característicos y los valores propios pero desde 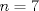 en adelante parece que hay problemas en calcular los valores propios. Es sencillo ver que en adelante parece que hay problemas en calcular los valores propios. Es sencillo ver que 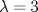 es valor propio (por qué?) pero qué pasa con el resto? es valor propio (por qué?) pero qué pasa con el resto?Eso, si alguien quiere jugar y tratar de comprobar si mi conjetura está bien o mal, bacán. Les estaré agradecidos y podré seguir viendo 9gag con la conciencia tranquila. Paz a todos. De hecho... si hubiese sido un sistema de 99x99 ahi tendriamos problemas. Algo me dice que si 3 divide a N, el kernel de la matriz planteada me parece que tiene dimension 2, porque usando el desarrollo de juancodmw, tendriamos solo 3 incognitas realmente y solo una ecuacion. Saludos Ceniciento. Claudio. -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 Jan 24 2015, 04:13 PM Jan 24 2015, 04:13 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 747 Registrado: 1-February 12 Miembro Nº: 100.827 Nacionalidad:  Universidad:  Sexo:  |
otra
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 09:03 PM |









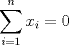
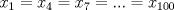
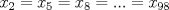
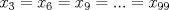
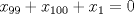 y
y 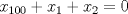 , se obtiene:
, se obtiene: 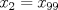 (1)
(1) y
y 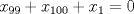 , se obtiene:
, se obtiene: 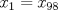 (2)
(2)