|
|
|
|
|
|
|
  |
 Jan 6 2015, 08:48 PM Jan 6 2015, 08:48 PM
Publicado:
#141
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 333 Registrado: 4-December 13 Desde: la jungla Miembro Nº: 125.821 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
saludos no quiero ser injusto, pero la explicación de vocin no la entendi -------------------- "Hay que ser listo, hay que ser escurridizo, hay que ser hábil" |
|
|
|
 Jan 6 2015, 09:02 PM Jan 6 2015, 09:02 PM
Publicado:
#142
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 783 Registrado: 23-April 13 Desde: Constitución Miembro Nº: 118.027 Nacionalidad:  Universidad:  Sexo:  |
ya, ahí les va:
Encuentre todos los números enteros positivos  tales que: tales que: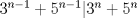 --------------------    |
|
|
|
 Jan 6 2015, 09:12 PM Jan 6 2015, 09:12 PM
Publicado:
#143
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
ya, ahí les va: Encuentre todos los números enteros positivos  tales que: tales que: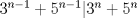 Suponga que 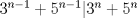 . Vea que . Vea que 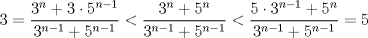 , lo que significa que , lo que significa que 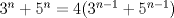 . Se sigue que . Se sigue que 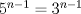 lo que deja como única posibilidad que lo que deja como única posibilidad que 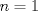 
-------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Jan 6 2015, 09:20 PM Jan 6 2015, 09:20 PM
Publicado:
#144
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 783 Registrado: 23-April 13 Desde: Constitución Miembro Nº: 118.027 Nacionalidad:  Universidad:  Sexo:  |
bien, nunca se me ocurren cosas asi xdd, propone
--------------------    |
|
|
|
 Jan 6 2015, 09:27 PM Jan 6 2015, 09:27 PM
Publicado:
#145
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Sea
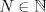 . Encuentre . Encuentre 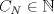 tal que la ecuación tal que la ecuación 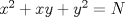 posea a lo más posea a lo más 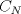 soluciones soluciones 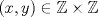 . . Observación: No les estoy pidiendo "la mejor cota", solo les pido una cota efectiva (aún cuando sea muy cerda o mala). Tengo en mente dos cotas distintas así que no me extrañaría que apareciera alguna otra forma de acotar. Mensaje modificado por Cenizas con Mostaza el Jan 6 2015, 09:39 PM -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Jan 7 2015, 11:23 AM Jan 7 2015, 11:23 AM
Publicado:
#146
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 76 Registrado: 31-May 14 Desde: mi casa Miembro Nº: 129.894 Nacionalidad:  Colegio/Liceo:  Sexo:  |
CITA 10 últimos mensajes [ en orden inverso ]Cenizas con Mostaza Escrito el Ayer, 09:27 PM Sea TEX: $N\in \mathbb{N}$. Encuentre TEX: $C_N\in \mathbb{N}$ tal que la ecuación TEX: $x^2+xy+y^2=N$ posea a lo más TEX: $C_N$ soluciones TEX: $(x,y)\in \mathbb{Z}\times\mathbb{Z}$. Observación: No les estoy pidiendo "la mejor cota", solo les pido una cota efectiva (aún cuando sea muy cerda o mala). Tengo en mente dos cotas distintas así que no me extrañaría que apareciera alguna otra forma de acotar. eeem (no entendi el enunciado, pero seria algo como esto??) Independiente de los valores que tomen X ,Y o N siempre podre resolver la ecuacion con a lo mas 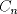 valores distintos de (x, y)? valores distintos de (x, y)? |
|
|
|
 Jan 7 2015, 11:45 AM Jan 7 2015, 11:45 AM
Publicado:
#147
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
eeem (no entendi el enunciado, pero seria algo como esto??) Independiente de los valores que tomen X ,Y o N siempre podre resolver la ecuacion con a lo mas 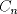 valores distintos de (x, y)? valores distintos de (x, y)?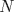 es un número fijo. Lo que pido es una cota superior de la cantidad de soluciones enteras de la ecuación es un número fijo. Lo que pido es una cota superior de la cantidad de soluciones enteras de la ecuación 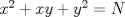 (o sea, un valor (o sea, un valor 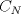 que depende de que depende de 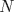 de modo que dicha ecuación no tenga más de de modo que dicha ecuación no tenga más de 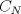 soluciones enteras). O sea, que esa cantidad de soluciones es finita. soluciones enteras). O sea, que esa cantidad de soluciones es finita.
-------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Jan 7 2015, 11:47 AM Jan 7 2015, 11:47 AM
Publicado:
#148
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 333 Registrado: 4-December 13 Desde: la jungla Miembro Nº: 125.821 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
eeem (no entendi el enunciado, pero seria algo como esto??) Independiente de los valores que tomen X ,Y o N siempre podre resolver la ecuacion con a lo mas 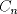 valores distintos de (x, y)? valores distintos de (x, y)?-------------------- "Hay que ser listo, hay que ser escurridizo, hay que ser hábil" |
|
|
|
 Jan 7 2015, 11:57 AM Jan 7 2015, 11:57 AM
Publicado:
#149
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Diste con la intuición que tenía en mente, eso recién es el principio. Ahora te falta concretar y dar una cota explícita del problema. -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Jan 7 2015, 01:00 PM Jan 7 2015, 01:00 PM
Publicado:
#150
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 333 Registrado: 4-December 13 Desde: la jungla Miembro Nº: 125.821 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
editado
Mensaje modificado por simio el Jan 7 2015, 01:48 PM -------------------- "Hay que ser listo, hay que ser escurridizo, hay que ser hábil" |
|
|
|
  |
3 usuario(s) está(n) leyendo esta discusión (3 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 04:26 PM |







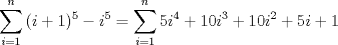
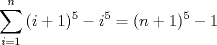 , luego:
, luego: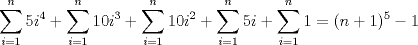
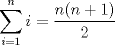
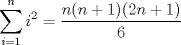
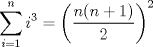
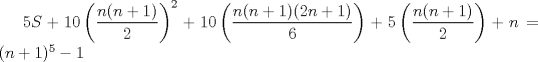
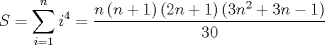





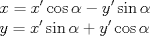
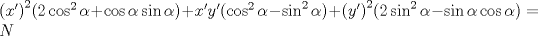
 de tal manera que el coeficiente del término x'y' sea 0
de tal manera que el coeficiente del término x'y' sea 0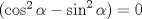
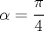
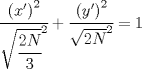
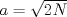 , e inscribible en una circunferencia de radio a
, e inscribible en una circunferencia de radio a![TEX: ${ C }_{ N }=4\left[ \sqrt { 2N } \right] +2 $](/tex-image/df34c78735c95c7e3f84b5d508472838.png) satisface
satisface