|
|
|
|
|
|
|
  |
 Jan 2 2015, 08:02 AM Jan 2 2015, 08:02 AM
Publicado:
#121
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 783 Registrado: 23-April 13 Desde: Constitución Miembro Nº: 118.027 Nacionalidad:  Universidad:  Sexo:  |
edit: la vendí brigido xd, donde ví tantos
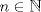 pensé q los términos de la sucesión también lo eran.. pensé q los términos de la sucesión también lo eran..
Mensaje modificado por juancodmw el Jan 2 2015, 10:22 AM --------------------    |
|
|
|
 Jan 2 2015, 09:57 AM Jan 2 2015, 09:57 AM
Publicado:
#122
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 333 Registrado: 4-December 13 Desde: la jungla Miembro Nº: 125.821 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
-------------------- "Hay que ser listo, hay que ser escurridizo, hay que ser hábil" |
|
|
|
 Jan 2 2015, 10:41 AM Jan 2 2015, 10:41 AM
Publicado:
#123
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
hipótesis pls considere 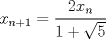 Supongo que esa sirve, no es así? Cómo la pillaste? Hay más? -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Jan 2 2015, 01:15 PM Jan 2 2015, 01:15 PM
Publicado:
#124
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Cabros, aún no veo respuesta satisfactoria así que les tiraré un par de observaciones que pueden servir de pista si pueden leer entre líneas.
La recurrencia se ve parecida a la sucesión de Fibonacci, pero no es lo mismo. Supongo que se dieron cuenta de eso y que son capaces de intentar escribir a mano unos cuantos términos de la sucesión (suponiendo conocido 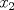 ). Asumo que son buenos observadores y pueden elaborar una conjetura dado cierto patrón, asumo también que ustedes saben jugar con inducción. Tampoco olviden la primera condición para restringir las cosas. ). Asumo que son buenos observadores y pueden elaborar una conjetura dado cierto patrón, asumo también que ustedes saben jugar con inducción. Tampoco olviden la primera condición para restringir las cosas.Ánimo cabros, este problema no es tan dificil. Si no se sienten muy motivados, más rato lo cambio a menos que alguien se oponga. -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Jan 2 2015, 01:53 PM Jan 2 2015, 01:53 PM
Publicado:
#125
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 325 Registrado: 18-March 14 Miembro Nº: 127.725 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
lo que nos sirve encontrar al final es la relación entre términos consecutivos de la sucesión, osea
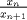 o bien o bien 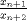 o lo que sea, tenemos o lo que sea, tenemos(1) 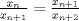 y 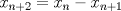 por hipotesis. por hipotesis.luego resolvemos para 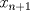 y queda lo de simio y queda lo de simio |
|
|
|
 Jan 2 2015, 02:05 PM Jan 2 2015, 02:05 PM
Publicado:
#126
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
-------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Jan 2 2015, 03:46 PM Jan 2 2015, 03:46 PM
Publicado:
#127
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Ok, ok, lo cambio.
Nuevo problema: En un torneo, cada equipo jugó 2 partidos contra cada uno de los restantes. Un solo equipo ganó el torneo, con 28 puntos, y exactamente 2 equipos quedaron últimos, con 22 puntos cada uno. Determinar cuántos equipos participaron en el torneo e indicar un posible desarrollo de los partidos, si se sabe que cada partido ganado otorga 2 puntos, cada partido perdido otorga 0 puntos y no hubo empates. -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Jan 2 2015, 05:12 PM Jan 2 2015, 05:12 PM
Publicado:
#128
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 333 Registrado: 4-December 13 Desde: la jungla Miembro Nº: 125.821 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Cabros, aún no veo respuesta satisfactoria así que les tiraré un par de observaciones que pueden servir de pista si pueden leer entre líneas. La recurrencia se ve parecida a la sucesión de Fibonacci, pero no es lo mismo. Supongo que se dieron cuenta de eso y que son capaces de intentar escribir a mano unos cuantos términos de la sucesión (suponiendo conocido 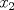 ). Asumo que son buenos observadores y pueden elaborar una conjetura dado cierto patrón, asumo también que ustedes saben jugar con inducción. Tampoco olviden la primera condición para restringir las cosas. ). Asumo que son buenos observadores y pueden elaborar una conjetura dado cierto patrón, asumo también que ustedes saben jugar con inducción. Tampoco olviden la primera condición para restringir las cosas.Ánimo cabros, este problema no es tan dificil. Si no se sienten muy motivados, más rato lo cambio a menos que alguien se oponga. la verdad a mi me dio mucha flojera escribir mi deducción, pero la intentaré explicar a continuación: existe un número  tal que tal que 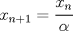 para cierto n, en nuestro caso n=1, luego para cierto n, en nuestro caso n=1, luego 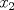 queda determinado y vale queda determinado y vale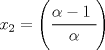 asi sucesivamente quedan todos los términos en función de  al escribir un par de términos va apareciendo el siguiente patrón: 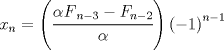 para n para n 3, donde 3, donde 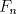 es el enésimo término en la sucesión de Fibonacci. es el enésimo término en la sucesión de Fibonacci.Si separamos la sucesión en términos con n par e impar notamos que se satisface que  para todo n si y solamente si para todo n si y solamente si 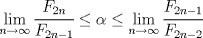 es sabido que 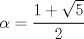 esop, saludines -------------------- "Hay que ser listo, hay que ser escurridizo, hay que ser hábil" |
|
|
|
 Jan 2 2015, 05:26 PM Jan 2 2015, 05:26 PM
Publicado:
#129
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Revisaré así a la rápida, así como escribiste a la rápida.
Me costó un poco entender las primeras 3 líneas pero está bien. Lo que viene después, bien, es una conjetura que involucra Fibonacci, ¿pero por qué es correcta? ¿Cómo lo justificas? Finalmente te falta detallar la conclusión. Pero en espíritu se ve bien (aunque no me deja satisfecho) pero ok. Disparas un propuesto o dejamos el que dejé como alternativa? Mensaje modificado por Cenizas con Mostaza el Jan 2 2015, 05:30 PM -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Jan 2 2015, 05:45 PM Jan 2 2015, 05:45 PM
Publicado:
#130
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 333 Registrado: 4-December 13 Desde: la jungla Miembro Nº: 125.821 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Ok, ok, lo cambio. Nuevo problema: En un torneo, cada equipo jugó 2 partidos contra cada uno de los restantes. Un solo equipo ganó el torneo, con 28 puntos, y exactamente 2 equipos quedaron últimos, con 22 puntos cada uno. Determinar cuántos equipos participaron en el torneo e indicar un posible desarrollo de los partidos, si se sabe que cada partido ganado otorga 2 puntos, cada partido perdido otorga 0 puntos y no hubo empates. ya cortito, sea x la cantidad de equipos del torneo, sabemos que la cantidad total de partidos en el torneo es de x(x-1), como cada partido entrega 2 puntos, la suma total de los puntajes del torneo sera 2x(x-1), además la cantidad mínima de puntaje total del torneo es de 28+22+22+24(x-3) y la máxima 28+22+22+26(x-3), inecuaciones mediante, x=13 -------------------- "Hay que ser listo, hay que ser escurridizo, hay que ser hábil" |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 2nd April 2025 - 08:51 PM |










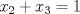 por lo que
por lo que 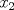 y
y 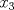 pueden tomar los valores de 0 y 1, ahora:
pueden tomar los valores de 0 y 1, ahora: 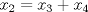 , si
, si 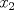 fuese 0,
fuese 0, 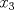 y
y 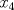 están obligados a ser 0 también, pero es absurdo pues
están obligados a ser 0 también, pero es absurdo pues 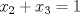 , se sigue que
, se sigue que 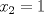 ,
, 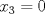 ,
, 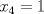 , ahora notemos que
, ahora notemos que 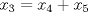 con lo que hemos obtenido, se tiene que
con lo que hemos obtenido, se tiene que 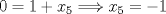 y esto ultimo nos manda todo al basurero, ya que no se cumple la condición
y esto ultimo nos manda todo al basurero, ya que no se cumple la condición 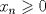 , por tanto no existe sucesión que cumpla con lo pedido.
, por tanto no existe sucesión que cumpla con lo pedido.
