demuestre - Foro fmat.cl

demuestre, conocido? no sé xdd

juancodmw Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 14 2014, 09:42 PM Publicado: #1
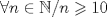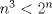
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 783 Registrado: 23-April 13 Desde: Constitución Miembro Nº: 118.027 Nacionalidad: Universidad: Sexo:	demuestre que $TEX: $\forall n\in \mathbb{N}/ n\geqslant 10$$ , $TEX: $n^{3}<2^{n}$$ --------------------

Adrianocor Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 14 2014, 10:02 PM Publicado: #2
Dios Matemático Grupo: Usuario FMAT Mensajes: 325 Registrado: 18-March 14 Miembro Nº: 127.725 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	doble Mensaje modificado por Adrianocor el Dec 14 2014, 10:08 PM

Adrianocor Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 14 2014, 10:02 PM Publicado: #3
Dios Matemático Grupo: Usuario FMAT Mensajes: 325 Registrado: 18-March 14 Miembro Nº: 127.725 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	forma terrible rápida suponemos que se cumple para n, osea que $TEX: \[\large n^{3}< 2^{n}\]<br />$ dado esto, par n+1 tenemos que: $TEX: \[\large (n+1)^{3}< 2\cdot 2^{n}\]$ luego, el lado derecho se duplicó, entonces basta comprobar que el lado izquierdo no se duplicó, especificamente: $TEX: \[\large (n+1)^{3}< 2\cdot n^{3}\]$ osea que: $TEX: \[\large n^{3}-3n^{2}-3n-1> 0\]<br />$ que es fácil ver que es creciente y positiva desde por lo menos 4 en adelante, y como n>=10 tamos listos Mensaje modificado por Adrianocor el Dec 14 2014, 10:03 PM

juancodmw Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 14 2014, 10:05 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 783 Registrado: 23-April 13 Desde: Constitución Miembro Nº: 118.027 Nacionalidad: Universidad: Sexo:	CITA(Adrianocor @ Dec 14 2014, 10:02 PM) forma terrible rápida suponemos que se cumple para n, osea que $TEX: \[\large n^{3}< 2^{n}\]<br />$ dado esto, par n+1 tenemos que: $TEX: \[\large (n+1)^{3}< 2\cdot 2^{n}\]$ luego, el lado derecho se duplicó, entonces basta comprobar que el lado izquierdo no se duplicó, especificamente: $TEX: \[\large (n+1)^{3}< 2\cdot n^{3}\]$ osea que: $TEX: \[\large n^{3}-3n^{2}-3n-1> 0\]<br />$ que es fácil ver que es creciente y positiva desde por lo menos 4 en adelante, y como n>=10 tamos listos esa era la idea, faltó demostrar lo ultimo, pero está bien edit: demuestren lo último que puso y estamos Mensaje modificado por juancodmw el Dec 14 2014, 10:07 PM --------------------

juancodmw Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 14 2014, 10:06 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 783 Registrado: 23-April 13 Desde: Constitución Miembro Nº: 118.027 Nacionalidad: Universidad: Sexo:	asdfg xd Mensaje modificado por juancodmw el Dec 14 2014, 10:06 PM --------------------

johb Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 14 2014, 10:06 PM Publicado: #6
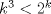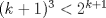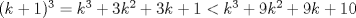Dios Matemático Grupo: Usuario FMAT Mensajes: 261 Registrado: 14-December 14 Miembro Nº: 134.911	Aplicamos induccion y tenemos que: i) Para n=k se tiene $TEX: $k^3<2^k$$ ii) Para n=k+1 se tiene $TEX: $(k+1)^3<2^{k+1}$$ para todo $TEX: $ k \leq 10 $$ Luego: $TEX: $ (k+1)^3=k^3+3k^2+3k+1 < k^3+9k^2+9k+10$$ (como k >=10) 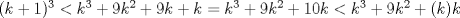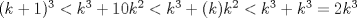$TEX: $(k+1)^3<k^3+9k^2+9k+k = k^3+9k^2+10k < k^3+9k^2+(k)k $$ $TEX: $(k+1)^3< k^3+10k^2 < k^3+(k)k^2 < k^3+k^3 = 2k^3$$ Pero por hipotesis tenemos que $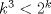TEX: $ k^3<2^k$$ , entonces: $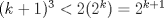TEX: $(k+1)^3<2(2^k) = 2^{k+1} $$ Por lo tanto por inducción demostramos que se cumple para cualquier n mayor o igual que 10. Tengo dos dias de vacaciones para entretenerme con estas cosiwis o Mensaje modificado por johb el Dec 14 2014, 10:07 PM -------------------- No estudio ingeniería.

juancodmw Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 14 2014, 10:10 PM Publicado: #7
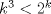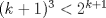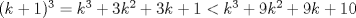Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 783 Registrado: 23-April 13 Desde: Constitución Miembro Nº: 118.027 Nacionalidad: Universidad: Sexo:	CITA(johb @ Dec 14 2014, 10:06 PM) Aplicamos induccion y tenemos que: i) Para n=k se tiene $TEX: $k^3<2^k$$ ii) Para n=k+1 se tiene $TEX: $(k+1)^3<2^{k+1}$$ para todo $TEX: $ k \leq 10 $$ Luego: $TEX: $ (k+1)^3=k^3+3k^2+3k+1 < k^3+9k^2+9k+10$$ (como k >=10) 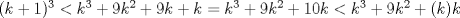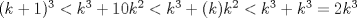$TEX: $(k+1)^3<k^3+9k^2+9k+k = k^3+9k^2+10k < k^3+9k^2+(k)k $$ $TEX: $(k+1)^3< k^3+10k^2 < k^3+(k)k^2 < k^3+k^3 = 2k^3$$ Pero por hipotesis tenemos que $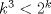TEX: $ k^3<2^k$$ , entonces: $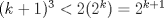TEX: $(k+1)^3<2(2^k) = 2^{k+1} $$ Por lo tanto por inducción demostramos que se cumple para cualquier n mayor o igual que 10. Tengo dos dias de vacaciones para entretenerme con estas cosiwis o wenaa, ahora si --------------------

Adrianocor Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 14 2014, 10:17 PM Publicado: #8
Dios Matemático Grupo: Usuario FMAT Mensajes: 325 Registrado: 18-March 14 Miembro Nº: 127.725 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(juancodmw @ Dec 14 2014, 10:05 PM) esa era la idea, faltó demostrar lo ultimo, pero está bien edit: demuestren lo último que puso y estamos sea $TEX: \[\large f(n)=n^{3}-3n^{2}-2n-1\]<br />$ tenemos que: $TEX: \[\large f(4)=3> 0\]<br />$ y luego $TEX: \[\large f'(n)=3n^{2}-6n-3\]<br />$ que es >0 para n>1+sqrt2 luego , como f(4) es positiva y su pendiente es mayor a 0 en el intervalo (1+sqrt2, +inf), f(x) es positiva en el intervalo que bos interesa (10, inf)

Adrianocor Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 14 2014, 10:17 PM Publicado: #9
Dios Matemático Grupo: Usuario FMAT Mensajes: 325 Registrado: 18-March 14 Miembro Nº: 127.725 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(juancodmw @ Dec 14 2014, 10:05 PM) esa era la idea, faltó demostrar lo ultimo, pero está bien edit: demuestren lo último que puso y estamos sea $TEX: \[\large f(n)=n^{3}-3n^{2}-2n-1\]<br />$ tenemos que: $TEX: \[\large f(4)=3> 0\]<br />$ y luego $TEX: \[\large f'(n)=3n^{2}-6n-3\]<br />$ que es >0 para n>1+sqrt2 luego , como f(4) es positiva y su pendiente es mayor a 0 en el intervalo (1+sqrt2, +inf), f(x) es positiva en el intervalo que bos interesa (10, inf)

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 3rd April 2025 - 11:38 PM