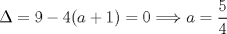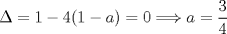|
|
|
|
|
|
|
  |
 Oct 22 2014, 06:16 PM Oct 22 2014, 06:16 PM
Publicado:
#1
|
|
 Doctor en Matemáticas Grupo: Colaborador Silver Mensajes: 193 Registrado: 17-August 12 Desde: Loncuma :3 Miembro Nº: 110.077 Nacionalidad:  Sexo:  |
XII Campeonato Escolar de Matemáticas Cuarto Nivel Cuarta prueba: Sábado 2 de Agosto, 2014 Problema 1: Encontrar los valores de  , de tal forma que la ecuación: , de tal forma que la ecuación: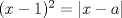 tenga exactamente tres soluciones reales diferentes. Problema 2: Sea 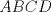 un cuadrado. Exteriormente se construyen los cuadrados un cuadrado. Exteriormente se construyen los cuadrados 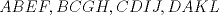 . El polígono . El polígono 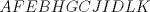 se denomina como cruz suiza. ¿Cuál es el mayor número de puntos de intersección que puede haber entre una cruz suiza y una línea recta que no contenga un lado de los cuadrados que forman la cruz? se denomina como cruz suiza. ¿Cuál es el mayor número de puntos de intersección que puede haber entre una cruz suiza y una línea recta que no contenga un lado de los cuadrados que forman la cruz?Disponible en formato PDF !!  Individual_N4.pdf ( 28.63k )
Número de descargas: 24
Individual_N4.pdf ( 28.63k )
Número de descargas: 24Saludos !! |
|
|
|
 Nov 22 2014, 11:07 AM Nov 22 2014, 11:07 AM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 783 Registrado: 23-April 13 Desde: Constitución Miembro Nº: 118.027 Nacionalidad:  Universidad:  Sexo:  |
P1 (no se si esté bn)
--------------------    |
|
|
|
 Nov 22 2014, 01:01 PM Nov 22 2014, 01:01 PM
Publicado:
#3
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 73 Registrado: 24-November 12 Miembro Nº: 113.337 Nacionalidad:  Universidad:  Sexo:  |
o que cada una tenga 2 soluciones reales, y una de ellas sea la misma para ambas
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 11th April 2025 - 07:43 AM |








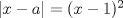
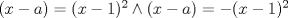
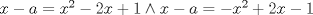
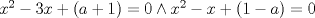
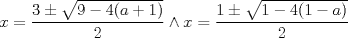
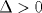 ) y que la segunda tenga 1 sola (
) y que la segunda tenga 1 sola (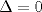 ), el 2do caso es lo mismo pero al revés..
), el 2do caso es lo mismo pero al revés..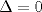 para ambas ecuaciones:
para ambas ecuaciones: