Prueba Final Nivel Mayor, 2014 Opciones

[pabl0paredes]

P3

 a123.png ( 8k ) Número de descargas:  1

Tomemos 3 puntos cualquiera y sus rectas L1, L2, L3, que estan trazadas tomando dos de ellos. Ahora los otros 2011 puntos pueden estar en A1, A2, A3 o A4. Si esta en A1, entonces al trazar las rectas con los tres puntos se observa que una de ellas corta al lado del triángulo formado que está sobre L2. Análogo pasará con A2 y L1, A3 y L3, y si está en A4 cortará a los tres lados del triángulo. 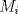Si analizamos estos casos, llamamos al número de puntos que hay en la región :

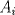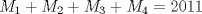Tenemos que , y tomando solo los casos mencionados, los cortes que se le habrán hecho al triángulo serán 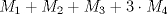, lo cual es un número impar ya que 2011 es impar y al multiplicar por 3 cualquier elemento de la suma no cambiará su paridad.

Falta el caso en que una recta formada por dos puntos cualquiera de los 2011 puntos restantes intersecte a lados del triángulo, pero como no hay 3 puntos colineales, entonces tales rectas intersectarán a 2 lados del triángulo o a ninguno, por lo tanto, no cambiará la paridad de la cantidad de cortes que se le hicieron al triángulo.

Como la suma de los cortes de cada lado del triángulo es impar, entonces al menos un lado del triángulo es cortado un número impar de veces.

Saludos

[Heiricar]

La idea del 5 puede ser usada para la primera parte de este problema , ¡Intenten los demás!