|
|
|
|
|
|
|
  |
 Nov 5 2005, 04:20 PM Nov 5 2005, 04:20 PM
Publicado:
#1
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Dados dos números naturales m y n, coprimos entre si, existen dos números enteros a y b tales que:
a • m + b • n = 1 Esta identidad se demuestra fácilmente usando por ejemplo el algoritmo de Euclides: se trata de hacer la división entera de m entre n (supongamos por ejemplo que m>n), e ir repitiendo esta división ahora entre n y el resto obtenido anteriormente, hasta llegar a resto 1. Esto es posible exactamente si los números m y n son coprimos entre si. Volviendo para atrás los pasos dados obtenemos la identidad de Bezout buscada. Vamos a hacerlo con un ejemplo concreto: Tomemos m=30 y n=13. Entonces 30=13•2+4 13=4•3+1 Por lo tanto 1=13 + 4•(-3)=13+ (30+13•(-2))•(-3)=(-3)•30+7•13 Luego los valores de a y b buscados son -3 y 7 respectivamente. Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Nov 5 2005, 09:11 PM Nov 5 2005, 09:11 PM
Publicado:
#2
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
De la identidad de Bezout a • m + b • n = 1 obtenemos, al aplicar congruencia módulo n, que a • m =1 (mod n), y por lo tanto que m tiene inverso módulo n igual a "a".
Por ejemplo, el inverso de 13 módulo 30 es igual a 7(observar el post anterior) Comentarios: Hablamos de los inversos de m (en modulo n) como aquelllos enteros "a" pertenecientes a Zn={0,1,2,...,n-1} tal que m • a=1(mod n) Por ejemplo en modulo 12 si nos preguntamos los inversos de 4,podriamos empezar probando para cada a perteneciente a Z12={0,1,2,...,11} 4 • 0=0(mod 12) 4 • 1=4(mod 12) 4 • 2=8(mod 12) 4 • 3=0(mod 12) 4 • 4=4(mod 12) 4 • 5=8(mod 12) 4 • 6=0(mod 12) 4 • 7=4(mod 12) 4 • 8=8(mod 12) 4 • 9=0(mod 12) 4 • 10=4(mod 12) 4 • 11=8(mod 12) Notamos por ende que el 4 NO TIENE INVERSO en Z12. Ahora si pensamos en (el)los inverso(s) de 5,nos encontraremos que: 5 • 0=0(mod 12) 5 • 1=5(mod 12) 5 • 2=10(mod 12) 5 • 3=3(mod 12) 5 • 4=8(mod 12) 5 • 5=1(mod 12) 5 • 6=6(mod 12) 5 • 7=11(mod 12) 5 • 8=4(mod 12) 5 • 9=9(mod 12) 5 • 10=2(mod 12) 5 • 11=7(mod 12) Notamos que el 5 si tiene inverso y este es UNICO.Esto se debe a que 5 y 12 son primos relativos(o bien coprimos) Notamos entonces que en Z12 tienen INVERSO UNICO aquellos que son primos relativos con 12 y los que no lo son..simplemente NO TIENEN INVERSO. Esto que solo lo decimos de forma muy superficial es posible de ser demostrado y espero poder hacerlo en alguna otra ocasion. Por ultimo noten que si estamos en Zp con p primo,entonces 1,2,3,4,....,p-1 seran primos relativos con p,y por ende todos sus elementos(salvo el 0) tendran un inverso y y este sera unico en Zp. Espero que esta reflexion les sea de ayuda para desarrollar la intuicion en cuanto a lo que a Zn se refiere(Poco a poco lo iremos "formalizando" mas,colocando las demostraciones de cada una de las cosas que se afirma aca "intuitivamente") Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jul 18 2012, 12:31 AM Jul 18 2012, 12:31 AM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Yo tenia entendido que la identidad de Bezout trabaja con m,n enteros no mecesariamente coprimos. ¿Estoy en lo correcto?
-------------------- Me voy, me jui.
|
|
|
|
 Jul 18 2012, 02:28 AM Jul 18 2012, 02:28 AM
Publicado:
#4
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 40 Registrado: 22-September 10 Desde: Cozumel, Quintana Roo, Mexico. Miembro Nº: 77.496 Nacionalidad:  Sexo:  |
En efecto se podria enunciar de la siguiente forma:
Dados m y n naturales entonces existen a y b enteros tales que: a*m+b*n=(m,n) Y el corolario cuando (m,n)=1 que se enuncio, su demostracion es analoga a la del corolario. Saludos. |
|
|
|
 Jul 18 2012, 10:08 AM Jul 18 2012, 10:08 AM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Yo tenia entendido que la identidad de Bezout trabaja con m,n enteros no mecesariamente coprimos. ¿Estoy en lo correcto? ya que existen los enteros a,b tales que am+bn=1... ¿existirán, crees tú, los enteros a', b' tales que a'n+b'm=mcd(m,n)? -------------------- |
|
|
|
 Jul 18 2012, 10:24 AM Jul 18 2012, 10:24 AM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
ya que existen los enteros a,b tales que am+bn=1... ¿existirán, crees tú, los enteros a', b' tales que a'n+b'm=mcd(m,n)? HAHAHAHAHAHAHAHAH -------------------- blep
|
|
|
|
 Jul 18 2012, 01:12 PM Jul 18 2012, 01:12 PM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
No tengo duda de aquello. Mi duda es si lo estàn enunciando ben aquí, nada más ;-)
Saludos. -------------------- Me voy, me jui.
|
|
|
|
 Nov 13 2012, 07:58 AM Nov 13 2012, 07:58 AM
Publicado:
#8
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 9 Registrado: 8-November 12 Miembro Nº: 112.665 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
tengo otra consulta que me serviría para resolver un problema que estoy haciendo
esta identidad de puede usar para tres números que con coprimos??? eso... saludos |
|
|
|
 Nov 13 2012, 08:43 AM Nov 13 2012, 08:43 AM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
tengo otra consulta que me serviría para resolver un problema que estoy haciendo esta identidad de puede usar para tres números que con coprimos??? eso... saludos Dados tres números naturales 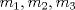 cuyo máximo divisor común es d, existen tres números enteros cuyo máximo divisor común es d, existen tres números enteros 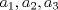 tales que tales que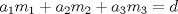 O sea, el resultado es válido para 3 números naturales. Cambiando "tres" por k, sigue siendo válido. -------------------- |
|
|
|
 Nov 13 2012, 09:17 AM Nov 13 2012, 09:17 AM
Publicado:
#10
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 9 Registrado: 8-November 12 Miembro Nº: 112.665 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
|
|
|
|
  |
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 03:41 AM |












