Identificarse Registrarse

Psu
Enseñanza Básica
Enseñanza Media
Universidad
Olimpiadas
Comunidad



 
 Reply to this topicStart new topic
> EDO no-lineal
Julio_fmat
mensaje Aug 16 2014, 04:45 AM
Publicado: #1


Dios Matemático Supremo
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 4.874
Registrado: 19-January 07
Desde: Mathematics!!
Miembro Nº: 3.830
Nacionalidad:
Colegio/Liceo: Liceo Comercial Los Angeles
Universidad: Universidad de Concepcion-FCFM
Sexo:



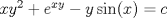Muestre que la relación TEX: $xy^2+e^{xy}-y\sin(x)=c$, proporciona soluciones implícitas para la EDO no-lineal dada por

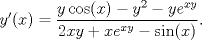TEX: $y'(x)=\dfrac{y\cos(x)-y^2-ye^{xy}}{2xy+xe^{xy}-\sin(x)}.$






--------------------


"... Lo veo, pero no puedo creerlo ... se trata de mostrar que las superficies, los volúmenes e incluso las variedades continuas de n dimensiones pueden ponerse en correspondencia unívoca con curvas continuas, o sea, con variedades de una sola dimensión, y que por consiguiente, las superficies, los volúmenes y las variedades de n dimensiones tienen también la misma potencia que las curvas ..."

G. Cantor.

Las Matemáticas son el lenguaje de la naturaleza, todo lo que nos rodea se puede representar y entender mediante números. Si se hace un gráfico con los números de un sistema, se forman modelos; éstos modelos están por todas partes en la naturaleza.

Max Cohen.


TEX: $$\Phi=\displaystyle \int \limits_{-\infty}^x \dfrac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}t^2}dt=\lim_{n\to +\infty}P\left(\dfrac{\displaystyle \sum_{i=1}^n x_i-n\mu}{n\sigma}\le x\right).$$



Licenciado en Matemática (2021). Universidad de Concepción, Chile.
Go to the top of the page
 
+Quote Post
XyipoxX
mensaje Nov 17 2015, 02:58 PM
Publicado: #2


Principiante Matemático
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 5
Registrado: 12-August 15
Miembro Nº: 139.677
Nacionalidad:
Colegio/Liceo: Liceo Manuel Barros Borgono
Universidad: Universidad de Santiago
Sexo:



Sólo hay que derivar de manera implícita la relación dada como sigue:

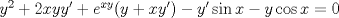TEX: $ y^2+2xyy'+e^{xy}(y+xy')-y'\sin x -y \cos x =0 $


Factorizando por 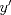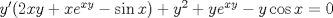TEX: $ y' $

TEX: $ y'(2xy+xe^{xy}-\sin x ) + y^2 +ye^{xy}-y\cos x =0 $


Así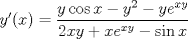

TEX: $ y'(x)=\displaystyle\frac{y\cos x -y^2 -y e^{xy}}{2xy+xe^{xy}-\sin x} $


Creo que eso es todo.

Saludos
Go to the top of the page
 
+Quote Post
johb
mensaje Nov 17 2015, 03:57 PM
Publicado: #3


Dios Matemático
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 261
Registrado: 14-December 14
Miembro Nº: 134.911
ayayai... hasta yo sabia hacer eso pu julio sad.gif, y eso que yo tuve dentro de calculo 3 un modulo de edos xD


--------------------
No estudio ingeniería.
Go to the top of the page
 
+Quote Post
 

Reply to this topicStart new topic
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):

 

Versión Lo-Fi Fecha y Hora actual: 4th April 2025 - 04:59 AM
Powered By IP.Board 2.2.1 © 2007  IPS, Inc.