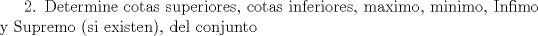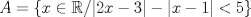Control 2 de Matemáticas 1. Bachillerato 2014

Control 2 de Matemáticas 1. Bachillerato 2014

Opciones

Vicarious Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 1 2014, 11:48 PM Publicado: #1
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 22 Registrado: 2-January 14 Miembro Nº: 126.296 Nacionalidad: Universidad: Sexo:	$TEX: \LARGE Control 2 de Matematicas 1$ $TEX: \large Programa Academico de Bachillerato. Universidad de Chile.$ $TEX: Tiempo: 15 minutos.$ $TEX: Nombre:$ $TEX: Elija solo un problema:$ $TEX: 1. Demuestre que:$ $TEX: $Si \left \| x-3 \right \|< 1$ entonces $\dfrac{1}{8}< \dfrac{1}{x+4}< \dfrac{1}{6}$$ $TEX: 2. 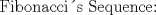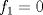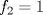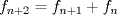Determine cotas superiores, cotas inferiores, maximo, minimo, Infimo y Supremo (si existen), del conjunto$ $TEX: $A= \left \{ x\in\mathbb{R} / {\left \| 2x-3 \right \|} - {\left \| x-1 \right \|}< 5 \right \}$$ -------------------- $TEX: Fibonacci´s Sequence:$ $TEX: $f_1=0$$ $TEX: $f_2=1$$ $TEX: $f_{n+2}= f_{n+1}+ f_{n}$$

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 2 2014, 12:05 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: $ $\\<br />El primero en una l\'inea y media:\\<br />$ $\\<br />$\|x-3\|<1\Longleftrightarrow 2<x<4\Longleftrightarrow 6<x+4<8$ y como $x>0$ podemos invertir quedando $\dfrac{1}{8}<\dfrac{1}{x+4}<\dfrac{1}{6}$.$ Mensaje modificado por Kaissa el Aug 2 2014, 12:06 PM -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

Lichiel Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 2 2014, 05:19 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 736 Registrado: 3-December 12 Miembro Nº: 113.971 Nacionalidad: Universidad: Sexo:	$TEX: \noindent P2. El conjunto $A=\{ x \in \mathbb{R}: \|2x-3\|-\|x-1\| < 5 =] -3,7 [ $. \\ Entonces el conjunto $L$ de cotas inferiores es $L=]-\infty, -3]$ y el conjunto de cotas superiores $R$ es $R=[7, +\infty [$ \\ Esto nos dice que A tiene supremo e infimo pues es no vácio y acotado. \\ Por otro lado $A$ es un intervalo abierto de números reales por lo tanto no tiene máximo ni mínimo con $\inf A =-3$ y $\sup A=7$ .$ -------------------- $TEX: \begin{center} $ \aleph_0$ $<$ $\|?\|$ $< \aleph_1 $ \end{center}$ $TEX: Teorema: Si 2 personas tienen el mismo RUT entonces son la misma o existe un delito o el registro civil cometió un error, Denuncie.$ Quiero plata

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 2 2014, 07:02 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	CITA(Lichiel @ Aug 2 2014, 05:19 PM) $TEX: \noindent P2. $A=\{ x \in \mathbb{R}: \|2x-3\|-\|x-1\| < 5\color{red}\}\color{black}=] -3,7 [ $, entonces el conjunto $L$ de cotas inferiores es $]-\infty, -3]$ y el conjunto de cotas superiores $R$ es $[7, +\infty [$. <br />\\Esto nos dice que $A$ tiene supremo e \'infimo pues es no vac\'io y acotado, finalmente $A$ es un intervalo abierto de números reales por lo tanto no tiene máximo ni mínimo con $\inf A =-3$ y $\sup A=7$ .$ Ahí quedó correctamente redactado Mensaje modificado por Kaissa el Aug 2 2014, 07:03 PM -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 4th April 2025 - 05:00 AM