Perpendiculares desde el foco.

Perpendiculares desde el foco.

Opciones

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 28 2014, 03:38 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: $ $\\<br />Sea $\mathcal{P}$ una par\'abola de foco $F$ y v\'ertice $V$.\\<br />Halle el lugar geom\'etrico que describe la proyecci\'on ortogonal desde $F$ hacia cualquier tangente a $\mathcal{P}$.$ -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

Adrianocor Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 28 2014, 06:52 PM Publicado: #2
Dios Matemático Grupo: Usuario FMAT Mensajes: 325 Registrado: 18-March 14 Miembro Nº: 127.725 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Hay que demostrarlo para todas las parabolas o basta para las horizontales y verticales?

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 28 2014, 08:50 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	CITA(Adrianocor @ Jul 28 2014, 06:52 PM) Hay que demostrarlo para todas las parabolas o basta para las horizontales y verticales? Demuestre que basta con UNO de esos dos casos para cubrirlos TODOS. -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

Diego_don_diego Ver Perfil del Miembro Ver los mensajes de este miembro	May 6 2015, 09:07 PM Publicado: #4
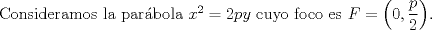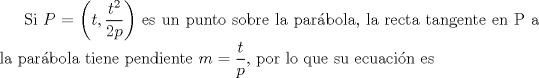Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 179 Registrado: 23-July 12 Desde: Algún lugar del mundo... 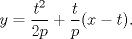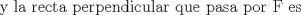Miembro Nº: 109.283 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	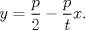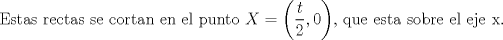$TEX: Consideramos la parábola $x^2=2py$ cuyo foco es $F=\left(0,\dfrac{p}{2}\right)$.$ $TEX: Si $P=\left(t,\dfrac{t^2}{2p}\right)$ es un punto sobre la parábola, la recta tangente en P a la parábola tiene pendiente $m=\dfrac{t}{p}$, por lo que su ecuación es$ $TEX: $y=\dfrac{t^2}{2p}+\dfrac{t}{p}(x-t).$$ $TEX: y la recta perpendicular que pasa por F es$ $TEX: $y=\dfrac{p}{2}-\dfrac{p}{t}x.$$ $TEX: Estas rectas se cortan en el punto $X=\left(\dfrac{t}{2},0\right)$, que esta sobre el eje x.$ Por tanto, el lugar geométrico de la proyección ortogonal de F sobre las tangentes a la parábola es la tangente a la parábola en su vértice.

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 4th April 2025 - 04:57 AM