|
|
|
|
|
|
|
  |
 May 14 2007, 12:58 PM May 14 2007, 12:58 PM
Publicado:
#1
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 39 Registrado: 6-August 05 Desde: Concepción Miembro Nº: 164 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Faltaba subir la prueba grupal
asi que aqui va Problema 1: El anciano Abuelo Anacleto tienen 10 hijos. Estos le dieron 70 nietos, los cuales han procreado ya 300 bisnietos. Anacleto lleva la cuenta exacta de sus tataranietos , que son 751 (hasta el momento). Demostrar que almenos 2 de los tataranietos del abuelo tienen el misnmo sexo y celebran su cumpleaños el mismo día del año. Problema 2: Considerar un triangulo isóceles ABC , con ABAC. sean D,E puntos en los lados AC,AB, respectivamente, tales que BC=BD y AD=DE=EB. Encontrar la medida del ángulo BAC. Problema 3: Calcular el valor de la siguiente multiplicación: 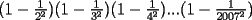 Problema 4: Demostrar que: 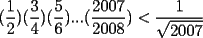 Problema 5: Considerar un mini tablero de ajedrez de 5x5 como el de la figura .  Hay una hormiga en el casillero marcado con una X.La hormiga camina sobre el tablero, pasando a cualquier casillero adyacente horizontal o verticalmente (no en diagonal). Determinar si la Hormiga puede partir en la posición X, pasar una y solo una vez por cada casillero del talero,para finalmente volver a su posición inicial. fin
Razón de edición: error tipeo en el P4
|
|
|
|
 May 14 2007, 06:45 PM May 14 2007, 06:45 PM
Publicado:
#2
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 329 Registrado: 24-August 06 Desde: Concepción Miembro Nº: 2.038 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Me gustaría saber cómo se hace el 4, que es el único que no sabría hacer.
Aprovecho para poner el que me tocó a mí (Estoy en M4, pero veo que las pruebas son iguales): 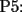 Primero que nada la hormiga recorre 26 cuadros. Los 25 del tablero, pero repitiendo el de la esquina. Vemos que la hormiga va alternando de cuadro blanco a negro a blanco, etc... Parte en uno blanco, así que el cuadro n-ésimo es blanco para n impar y negro para n par. El último cuadro que el el 26° es negro y no coincide con el primero (que se dijo era blanco). Así que la hormiga no puede realizar el recorrido pedido. |
|
|
|
 May 14 2007, 08:00 PM May 14 2007, 08:00 PM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747 |
Respuesta censurada
error feo..y el propuesto estaba malo .. disculpas pertinentes Mensaje modificado por jorgeston el May 14 2007, 10:19 PM |
|
|
|
 May 14 2007, 08:10 PM May 14 2007, 08:10 PM
Publicado:
#4
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 54 Registrado: 21-April 07 Miembro Nº: 5.372 Nacionalidad:  Sexo:  |
Ja! A mí igual me tocó el 4. Muy peludo
Pero llegué a la conclusión que era mayor que 1/2007 después porque: Probando: (1/2)(3/4)(5/6) < 1/6 15/48 = 5/16 > 1/6 (15/48)(7/8)(9/10) = 945/3840 = 0,24609375 (me dio lata simplificar 0,24609375 > 0.1 945/3840 > 1/10 Así siguiendo con esa técnica llegaríamos a que el tremendo número es MAYOR a 1/2007 También se me ocurrió hacerlo con factoriales: los pares (los de abajo) vendrían siendo: 2(1004!), porque así son sólo los pares hasta 2*1004 = 2008 y los impares (los de arriba) sería: 2007! - pares; osea, 2007! - 2(1004!) Osea, la inecuación (nuestra duda) sería: 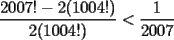 También sabemos que el producto de los impares es menor al de los pares, por lo que SABEMOS que 2007! - 2(1004!) < 2(1004!) 2007! < 4(1004!) 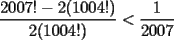 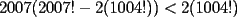 Y eso, no sé cómo seguir xd, o la verdad me cansé. En fin, la cosa es que es mayor |
|
|
|
 May 14 2007, 08:54 PM May 14 2007, 08:54 PM
Publicado:
#5
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 329 Registrado: 24-August 06 Desde: Concepción Miembro Nº: 2.038 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Ok. Ahora me quedó claro.
[EDIT]: =0!! ¡entonces no era esa! Bueno, igual gracias. Y aprovechando el post: Acá va el 3: Realizando las restas: 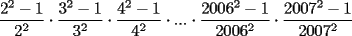 Usando suma por diferencia y separando los cuadrados: 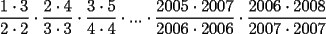 Simplificando los numeradores con los denominadores de las fracciones adyacentes: 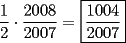
Mensaje modificado por Manuel71 el May 15 2007, 06:56 AM |
|
|
|
 May 14 2007, 10:01 PM May 14 2007, 10:01 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
En el 4, para salir del paso rapido aproxime resultado del producto a
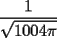 con un error muy pequeño. Este numero es mayor que la cota propuesta asi que lo mas probable es que el ejercico este malo. con un error muy pequeño. Este numero es mayor que la cota propuesta asi que lo mas probable es que el ejercico este malo.Si alguien dispone de tiempo intente demostrar la desigualdad en el otro sentido (induccion?) Saludos -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 May 14 2007, 11:05 PM May 14 2007, 11:05 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 817 Registrado: 28-May 06 Desde: maipú, santiago. Miembro Nº: 1.210 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
 -------------------- Estudiante de 5º año de Ingeniería Civil Industrial en la U. de Chile
|
|
|
|
 May 15 2007, 12:01 AM May 15 2007, 12:01 AM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
Solo notar que mirando los inversos multiplicativos, el del producto es
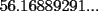 (calculado con Derive) mientras que mi aproximacion da (calculado con Derive) mientras que mi aproximacion da 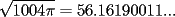 (!!?) y el del lado derecho es (obviamente) (!!?) y el del lado derecho es (obviamente) 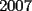 . .Me llamo la atencion... Saludos -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 May 15 2007, 05:55 PM May 15 2007, 05:55 PM
Publicado:
#9
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 1 Registrado: 15-May 07 Miembro Nº: 5.873 Nacionalidad:  Sexo:  |
También se me ocurrió hacerlo con factoriales: los pares (los de abajo) vendrían siendo: [/color]2(1004!), porque así son sólo los pares hasta 2*1004 = 2008 y los impares (los de arriba) sería: 2007! - pares; osea, 2007! - 2(1004!) Osea, la inecuación (nuestra duda) sería: [tex]$dfrac\{2007! - 2(1004!)}{2(1004!)} < \dfrac{1}{2007}$[tex] También sabemos que el producto de los impares es menor al de los pares, por lo que SABEMOS que 2007! - 2(1004!) < 2(1004!) 2007! < 4(1004!) [tex]$dfrac\{2007! - 2(1004!)}{2(1004!)} < \dfrac{1}{2007}$[tex] [tex]$2007(2007! - 2(1004!))< 2(1004!) $[tex] Y eso, no sé cómo seguir xd, o la verdad me cansé. En fin, la cosa es que es mayor Creo que ahi esta mal... ya que en los denominadores tendrias: (1x2) (2x2) (3x2).... (1004x2) Si quieres sacar factor comun 2, tienes 1004 mutiplicaciones, quedaria en potencia... osea: 21004 x 1004! Lo otro... Para sacar los numeros impares... Seria: 2007! / 21003 x 1003! (1003 porque si fuera 1004 estarias contando el 2008... entonces te quedarian todos los n° impares hasta 2007 / 2008) Y luego te quedaria... 2007! 22007 x 1004! x 1003! (No se como hacer la raya fraccionaria XD) Saludos! |
|
|
|
| Cesarator |
 May 15 2007, 08:32 PM May 15 2007, 08:32 PM
Publicado:
#10
|
|
Invitado |
En el p4, como ya vieron, hubo un error de tipeo, la intención original era pedir demostrar que el producto es menor que
![TEX: \[\frac{1}{\sqrt {2007}}\]](./tex/1179279221.gif) .. se perdió la raíz en el tipeo... |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 11th April 2025 - 08:07 AM |











